题目内容
正三棱柱有一个半径为
cm的内切球，则此棱柱的体积是（ ）
| 3 |
A、9
| ||
| B、54cm3 | ||
| C、27cm3 | ||
D、18
|
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：由题意知正三棱柱的高为2
cm，底面正三角形的内切圆的半径为
cm，底面正三角形的边长为6cm，由此能求出此正三棱柱的体积．
| 3 |
| 3 |
解答：
解：∵正三棱柱有一个半径为
cm的内切球，
∴由题意知正三棱柱的高为2
cm，
底面正三角形的内切圆的半径为
cm，
底面正三角形的边长为6cm，
∴正三棱柱的底面面积为9
cm2，
故此正三棱柱的体积V=9
×2
=54（cm3）．
故选：B．
| 3 |
∴由题意知正三棱柱的高为2
| 3 |
底面正三角形的内切圆的半径为
| 3 |
底面正三角形的边长为6cm，
∴正三棱柱的底面面积为9
| 3 |
故此正三棱柱的体积V=9
| 3 |
| 3 |
故选：B．
点评：本题考查棱柱的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
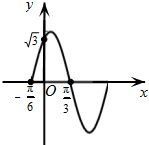如图，函数f（x）=Asin（ωx+φ），x∈R，（其中A＞0，ω＞0，0≤φ≤
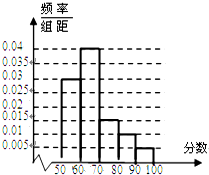在某中学举行的环保知识竞赛中，将三个年级参赛的学生的成绩进行整理后分为5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组，已知第二小组的频数是40，则成绩在80～100分的学生人数是（ ）