题目内容
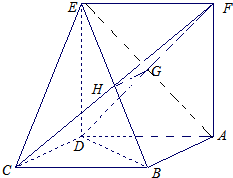 平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.(1)求证:BD⊥平面CDE;
(2)求证:GH∥平面CDE;
(3)求三棱锥D-CEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知得ED⊥平面ABCD,从而ED⊥BD.又BD⊥CD,由此能证明BD⊥平面CDE.
(2)连结EA,则GH∥AB,由此能证明GH∥平面CDE.
(3)由VD-CEF=VC-DEF,利用等积法能求出三棱锥D-CEF的体积.
(2)连结EA,则GH∥AB,由此能证明GH∥平面CDE.
(3)由VD-CEF=VC-DEF,利用等积法能求出三棱锥D-CEF的体积.
解答:
(1)证明:平面ADEF⊥平面ABCD,交线为AD.
∵ED⊥AD,∴ED⊥平面ABCD.
∴ED⊥BD.又∵BD⊥CD,∴BD⊥平面CDE.
(2)证明:连结EA,则G是AE的中点.
∴△EAB中,GH∥AB.又∵AB∥CD,
∴GH∥CD,∴GH∥平面CDE.
(3)解:设Rt△BCD中BC边上的高为h.
∵CD=1,∠BCD=60°,∴BC=2,h=
.
即:点C到平面DEF的距离为
,
∴VD-CEF=VC-DEF=
•
•2•2•
=
.

∵ED⊥AD,∴ED⊥平面ABCD.
∴ED⊥BD.又∵BD⊥CD,∴BD⊥平面CDE.
(2)证明:连结EA,则G是AE的中点.
∴△EAB中,GH∥AB.又∵AB∥CD,
∴GH∥CD,∴GH∥平面CDE.
(3)解:设Rt△BCD中BC边上的高为h.
∵CD=1,∠BCD=60°,∴BC=2,h=
| ||
| 2 |
即:点C到平面DEF的距离为
| ||
| 2 |
∴VD-CEF=VC-DEF=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
点评:本题考查直线与平面垂直的证明,考查直线与平面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知椭圆
+
=1与双曲线
-
=1有相同的焦点,则动点P(n,m)的轨迹( )
| x2 |
| 9 |
| y2 |
| n |
| x2 |
| 4 |
| y2 |
| m |
| A、椭圆的一部分 |
| B、双曲线的一部分 |
| C、抛物线的一部分 |
| D、直线的一部分 |
下图是对数函数y=logax的图象,已知a的值取
、
、2、5,则相应于C1、C2、C3、C4的a的值依次是( )

| 1 |
| 3 |
| 2 |
| 3 |

A、
| ||||
B、
| ||||
C、5、2、
| ||||
D、5、2、
|
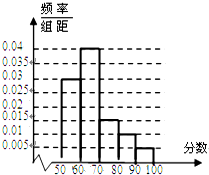 在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )
在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )| A、15 | B、18 | C、20 | D、25 |
下列说法正确的是( )
| A、φ?{0} |
| B、0⊆Φ |
| C、0∈{(0,1)} |
| D、(1,2)∈{1,2,3} |
 设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥面ABCD.
设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥面ABCD.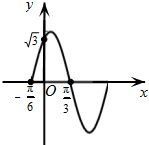 如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤
如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤