题目内容
已知抛物线C的准线方程为x=-
.
(Ⅰ)求抛物线C的标准方程;
(Ⅱ) 若过点P(t,0)的直线l与抛物线C相交于A、B两点,且以AB为直径的圆过原点O,求证t为常数,并求出此常数.
| 1 |
| 4 |
(Ⅰ)求抛物线C的标准方程;
(Ⅱ) 若过点P(t,0)的直线l与抛物线C相交于A、B两点,且以AB为直径的圆过原点O,求证t为常数,并求出此常数.
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)直接利用抛物线的准线方程,求解抛物线C的标准方程即可;
(Ⅱ)设出直线方程与抛物线联立,转化原点O落在以AB为直径的圆上,得到
•
=0,求出t的值即可证明结果.
(Ⅱ)设出直线方程与抛物线联立,转化原点O落在以AB为直径的圆上,得到
| OA |
| OB |
解答:
解:(Ⅰ)由准线方程为x=-
可设抛物线C的方程y2=2px,(p>0).
求得p=
,…(2分)
故所求的抛物线C的方程为:y2=x; …(4分)
(Ⅱ)证明:依题意可设过P的直线l方程为:x=my+t(m∈R),…(6分)
设A(x1,y1),B(x2,y2)
由
得:y2=my+t,
依题意可知△>0恒成立,且y1•y2=-t,…(8分)
原点O落在以AB为直径的圆上.
令
•
=0即x1x2+y1y2=(y1•y2)2+y1•y2=(-t)2-t=0.…(10分)
解得:t=1,t=0即t为常数,∴原题得证. …(12分)
(说明:直线l方程也可设为:y=k(x-t),但需加入对斜率不存在情况的讨论,否则扣1分)
| 1 |
| 4 |
求得p=
| 1 |
| 2 |
故所求的抛物线C的方程为:y2=x; …(4分)
(Ⅱ)证明:依题意可设过P的直线l方程为:x=my+t(m∈R),…(6分)
设A(x1,y1),B(x2,y2)
由
|
依题意可知△>0恒成立,且y1•y2=-t,…(8分)
原点O落在以AB为直径的圆上.
令
| OA |
| OB |
解得:t=1,t=0即t为常数,∴原题得证. …(12分)
(说明:直线l方程也可设为:y=k(x-t),但需加入对斜率不存在情况的讨论,否则扣1分)
点评:本题考抛物线的标准方程的求法,直线与椭抛物线的位置关系,抛物线方程的综合应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
下列函数中,不是幂函数的是( )
| A、y=2x | ||
| B、y=x-1 | ||
C、y=
| ||
| D、y=x3 |
下图是对数函数y=logax的图象,已知a的值取
、
、2、5,则相应于C1、C2、C3、C4的a的值依次是( )

| 1 |
| 3 |
| 2 |
| 3 |

A、
| ||||
B、
| ||||
C、5、2、
| ||||
D、5、2、
|


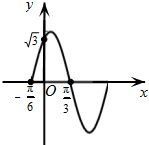 如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤
如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤