在极坐标系中.极点到直线ρcosθ=1的距离为1．题目和参考答案——青夏教育精英家教网——

题目内容

17．在极坐标系中，极点到直线ρcosθ=1的距离为1．

分析先求出直线的直角坐标方程，求出极点的直角坐标，即可求得极点到直线ρcosθ=1的距离．

解答解：直线ρcosθ=1，即x=1，极点的直角坐标为（0，0），故极点到直线ρcosθ=1的距离为1，
故答案为1．

点评本题主要考查把点的极坐标化为直角坐标，点到直线的距离的定义，属于基础题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

7．已知点A（0，2），抛物线C：y²=mx（m＞0）的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，若|FM|：|MN|=1：2，则△OFN的面积为（　　）

$\frac{8\sqrt{3}}{3}$

$\frac{4\sqrt{3}}{3}$

8．某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数作为样本进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100）的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100）的数据）

（Ⅰ）求样本容量n和频率分布直方图中x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学到市政广场参加环保宣传的志愿者活动，求所抽取的2名同学来自不同组的概率．

5．在直角坐标系xOy中，曲线C₁的方程为$\frac{x^2}{9}+{y^2}=1$．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C₂的极坐标方程为ρ²-8ρsinθ+15=0．
（Ⅰ）写出C₁的参数方程和C₂的直角坐标方程；
（Ⅱ）设点P在C₁上，点Q在C₂上，求|PQ|的最大值．

12．某中学高一、高二年级各有8个班，学校调查了春学期各班的文学名著阅读量（单位：本），并根据调查结果，得到如下所示的茎叶图：

为鼓励学生阅读，在高一、高二两个两个年级中，学校将阅读量高于本年级阅读量平均数的班级命名为该年级的“书香班级”．
（1）当a=4时，记高一年级“书香班级”数为m，高二年级的“书香班级”数为n，比较m，n的大小关系；
（2）在高一年级8个班级中，任意选取两个，求这两个班级均是“书香班级”的概率；
（3）若高二年级的“书香班级”数多于高一年级的“书香班级”数，求a的值（只需写出结论）

2．下列函数中，既是偶函数又是（0，+∞）上的增函数的是（　　）

y=${x}^{\frac{1}{2}}$

y=log₃（-x）

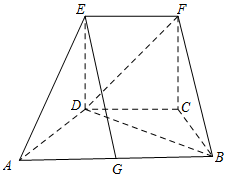如图所示的几何体中，四边形ABCD为等腰梯形，AB∥CD，AB=2AD=2，∠DAB=60°，四边形CDEF为正方形，平面CDEF⊥平面ABCD．
（Ⅰ）若点G是棱AB的中点，求证：EG∥平面BDF；
（Ⅱ）求直线AE与平面BDF所成角的正弦值；
（Ⅲ）在线段FC上是否存在点H，使平面BDF⊥平面HAD？若存在，求$\frac{FH}{HC}$的值；若不存在，说明理由．

6．在复平面内，复数z的对应点为（1，2），复数z的共轭复数为（　　）

7．已知复数z满足（3-i）z=2+i（i为虚数单位），则z的共轭复数是（　　）

$\frac{1}{2}$+$\frac{1}{2}$i

$\frac{1}{2}$-$\frac{1}{2}i$

-$\frac{1}{2}$+$\frac{1}{2}$i

-$\frac{1}{2}$-$\frac{1}{2}$i