题目内容
19.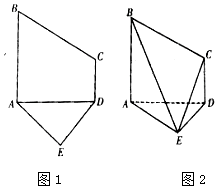 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.(Ⅰ)若M为DE中点,边BC上是否存在一点N,使得MN∥平面ABE?若存在,求$\frac{BN}{BC}$的值;若不存在,说明理由;
(Ⅱ)求四面体B-CDE的体积.
分析 (Ⅰ)取BC中点为N,AD中点为P,连接MN,NP,MP.推导出MP∥面ABE,NP∥面ABE,由此能求出边AB上存在一点N,使得MN∥平面ABE,且$\frac{BN}{BC}=\frac{1}{2}$.
(Ⅱ)推导出EP⊥AD,由四面体B-CDE的体积VB-CDE=VE-BCD,能求出结果.
解答 解:(Ⅰ)取BC中点为N,AD中点为P,连接MN,NP,MP.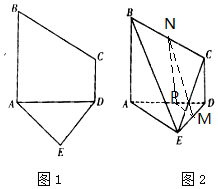
∵MP∥AE,AE⊆面ABE,MP?面ABE,
∴MP∥面ABE,同理NP∥面ABE,
又MP∩NP=P,∴MN∥面ABE,
∴边AB上存在一点N,使得MN∥平面ABE,且$\frac{BN}{BC}=\frac{1}{2}$.
(Ⅱ)∵△ADE为等腰直角三角形.
∴EP⊥AD,
又平面ABCD平面ADE,∴EP⊥平面ABCD,
∵$EP=\sqrt{2}$,${S_{△BCD}}=2\sqrt{2}$,
∴四面体B-CDE的体积VB-CDE=VE-BCD=$\frac{1}{3}×EP×{S_{△BCD}}$=$\frac{1}{3}×\sqrt{2}×2\sqrt{2}=\frac{4}{3}$.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想,数形结合思想,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.已知集合A={0,1,2},B={x|1≤x≤4},集合A∩B=( )
| A. | ∅ | B. | {1,2} | C. | [1,2] | D. | (1,2) |
10.已知函数f(x)=xlnx+x(x-a)2(a∈R),若存在$x∈[{\frac{1}{2},2}]$,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
| A. | $({\frac{9}{4},+∞})$ | B. | $({\frac{3}{2},+∞})$ | C. | $({\sqrt{2},+∞})$ | D. | (3,+∞) |
14.设倾斜角为α的直线l经过抛物线C:y2=2px(p>0)的焦点F,与抛物线C交于A,B两点,设点A在x轴上方,点B在x轴下方.若$\frac{|AF|}{|BF|}=m$,则cosα的值为( )
| A. | $\frac{m-1}{m+1}$ | B. | $\frac{m}{m+1}$ | C. | $\frac{m-1}{m}$ | D. | $\frac{{2\sqrt{m}}}{m+1}$ |
4.已知点A(-1,-2)在抛物线C:y2=2px的准线上,记C的焦点为F,过点F且与x轴垂直的直线与抛物线交于M,N两点,则线段MN的长为( )
| A. | 4 | B. | $2\sqrt{3}$ | C. | 2 | D. | 1 |
8.已知等比数列{an}的前n项和为Sn,则“a1>0”是“S2017>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超
过0.01的前提下认为“课外体育达标”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望.
独立性检验界值表:
(参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
| 平均每天锻炼 的时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
| 总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超
过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 20 | 110 | |
| 合计 |
独立性检验界值表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |