题目内容
9.某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)| 平均每天锻炼 的时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
| 总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超
过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 20 | 110 | |
| 合计 |
独立性检验界值表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
分析 (1)根据所给数据,可得列联表,计算K2,即可得出结论;
(2)将频率视为概率,X~B(3,0.25),即可求X的数学期望.
解答 解:(1)列出列联表,
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
所以在犯错误的概率不超过0.01的前提下不能判断“课外体育达标”与性别有关.
(2)由表中数据可得,抽到“课外体育达标”学生的概率为0.25,
将频率视为概率,∴X~B(3,0.25),
∴$E(X)=3×\frac{1}{4}=\frac{3}{4}$.
点评 本题考查独立性检验知识的运用,考查求X的数学期望,属于中档题.

练习册系列答案
相关题目
17.已知集合A={x|x>0},B={x|x2-2x-3<0},则A∩B=( )
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
14.若等差数列{an}的前n项和Sn满足S4≤4,S6≥12,则a4的最小值为( )
| A. | 2 | B. | $\frac{7}{2}$ | C. | 3 | D. | $\frac{5}{2}$ |
1.已知f(x)=$\frac{e^x}{{{x^2}+a}}({a>0})$的两个极值点分别为x1,x2(x1<x2),则a(lnx1+lnx2)的取值范围是( )
| A. | $[{-\frac{1}{e},0})$ | B. | (0,+∞) | C. | (0,1) | D. | $[{-\frac{1}{e},+∞})$ |
19.(3-2x-x4)(2x-1)6的展开式中,含x3项的系数为( )
| A. | 600 | B. | 360 | C. | -600 | D. | -360 |
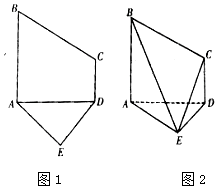 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.