题目内容
已知点P是函数f(x)=cosx(0≤x≤
)图象上一点,则曲线y=f(x)在点P处的切线斜率的最小值为 .
| π |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,三角函数的求值
分析:求出函数的导数,求出切线的斜率,再由正弦函数的单调性,即可求得范围.
解答:
解:函数f(x)=cosx的导数f′(x)=-sinx,
设P(m,cosm),则曲线y=f(x)在点P处的切线斜率为f′(m)=-sinm,
由于0≤m≤
,则0≤sinm≤
,
则-
≤-sinm≤0,
则在点P处的切线斜率的最小值为-
.
故答案为:-
.
设P(m,cosm),则曲线y=f(x)在点P处的切线斜率为f′(m)=-sinm,
由于0≤m≤
| π |
| 3 |
| ||
| 2 |
则-
| ||
| 2 |
则在点P处的切线斜率的最小值为-
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题考查导数的几何意义,考查运用三角函数的性质求切线的斜率的范围,考查运算能力,属于中档题.

练习册系列答案
相关题目
若|
|=
,|
|=2,(
-
)⊥
,则
,
的夹角是( )
| a |
| 2 |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
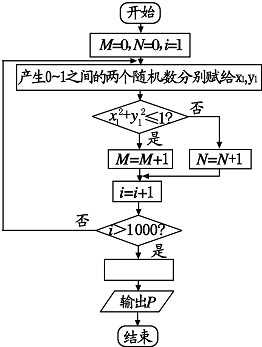
如图所示,使用模拟方法估计圆周率值的程序框图,P表示估计的结果,则图中空白框内应填入P=( )

A、
| ||
B、
| ||
C、
| ||
D、
|