题目内容
已知C52=C20C32+C21C31+C22C30;C83=C40C43+C41C42+C42C41+C43C40;C94=C30C64+C31C63+C32C62+C33C61
观察以上等式的规律,在横线处填写一个合适的式子使得下列等式成立,C103=C40C63+ .
观察以上等式的规律,在横线处填写一个合适的式子使得下列等式成立,C103=C40C63+
考点:归纳推理
专题:推理和证明
分析:仔细观察所给等式,我们能够发现:拆分后的每个加数中两个组合数的上标之和、下标之和分别等于拆分前组合数的上标、下标,根据此规律,得到
的表达式即可.
| C | 3 10 |
解答:
解:根据所给等式,可得
拆分后的每个加数中两个组合数的上标之和、下标之和分别等于拆分前组合数的上标、下标,
所以C103=C40C63+
.
故答案为:
.
拆分后的每个加数中两个组合数的上标之和、下标之和分别等于拆分前组合数的上标、下标,
所以C103=C40C63+
| 2 6 |
| 1 6 |
| 0 6 |
故答案为:
| 2 6 |
| 1 6 |
| 0 6 |
点评:本题主要考查了归纳推理的灵活运用,解答此题的关键是注意观察所给等式,从中找出规律并利用它求出其它的组合数的表达式.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
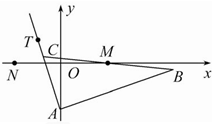 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
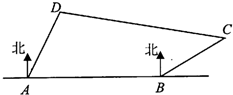 如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3
如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3