题目内容
已知正四棱锥S-ABCD中,AB=2,则当该棱锥外接球体积最小时,它的高等于 .
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:设棱锥外接球的半径为R,高为h,则该棱锥外接球体积最小时,R最小.由题意,可得h(2R-h)=2,利用基本不等式可得2≤(
)2,即可得出结论.
| h+2R-h |
| 2 |
解答:
解:设棱锥外接球的半径为R,高为h,则该棱锥外接球体积最小时,R最小.
∵正四棱锥S-ABCD中,AB=2,
∴R2=(h-R)2+2,
∴h(2R-h)=2,
∴2≤(
)2,
即R≥
,
当且仅当h=2R-h,即h=R=
时,R最小.
故答案为:
.
∵正四棱锥S-ABCD中,AB=2,
∴R2=(h-R)2+2,
∴h(2R-h)=2,
∴2≤(
| h+2R-h |
| 2 |
即R≥
| 2 |
当且仅当h=2R-h,即h=R=
| 2 |
故答案为:
| 2 |
点评:本题考查棱柱、棱锥、棱台的体积,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
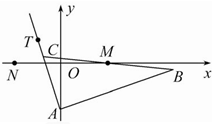 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足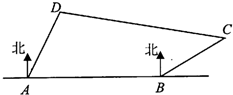 如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3
如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3