题目内容
已知曲线C:x2+y2=1,对它先作矩阵A=
对应的变换,再作矩阵B=
对应的变换,得到曲线C:
+y2=1.则实数b= .
|
|
| x2 |
| 4 |
考点:复合变换与二阶矩阵的乘法
专题:选作题,矩阵和变换
分析:从曲线C1变到曲线C2的变换对应的矩阵为BA,然后在曲C1上任意选一点P(x0,y0),设它在矩阵BA对应的变换作用下变为P'(x',y'),建立关系式,将P(x0,y0)代入x2+y2=1,最后与
+y2=1比较可得b的值.
| x2 |
| 4 |
解答:
解:从曲线C1变到曲线C2的变换对应的矩阵BA=
•
=
在曲C1上任意选一点P(x0,y0),设它在矩阵BA对应的变换作用下变为P'(x',y'),
则有
•
=
解得
代入曲线C:x2+y2=1,得,y'2+(
x′)2=1
即曲线方程为:
+y2=1
与已知的曲线C2的方程为:
+y2=1比较得(2b)2=4
所以b=±1.
故答案为:±1.
|
|
|
在曲C1上任意选一点P(x0,y0),设它在矩阵BA对应的变换作用下变为P'(x',y'),
则有
|
|
|
解得
|
| 1 |
| 2b |
即曲线方程为:
| x2 |
| 4b2 |
与已知的曲线C2的方程为:
| x2 |
| 4 |
所以b=±1.
故答案为:±1.
点评:本题主要考查了矩阵变换的性质,同时考查了计算能力和运算求解的能力,属于基础题.

练习册系列答案
相关题目
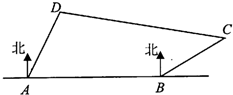 如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3
如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3