题目内容
若α,β为两个不同的平面,m、n为不同直线,下列推理:
①若α⊥β,m⊥α,n⊥β,则直线m⊥n;
②若直线m∥平面α,直线n⊥直线m,则直线n⊥平面α;
③若直线m∥n,m⊥α,n?β,则平面α⊥平面β;
④若平面α∥平面β,直线m⊥平面β,n?α,则直线m⊥直线n;
其中正确说法的序号是( )
①若α⊥β,m⊥α,n⊥β,则直线m⊥n;
②若直线m∥平面α,直线n⊥直线m,则直线n⊥平面α;
③若直线m∥n,m⊥α,n?β,则平面α⊥平面β;
④若平面α∥平面β,直线m⊥平面β,n?α,则直线m⊥直线n;
其中正确说法的序号是( )
| A、③④ | B、①③④ |
| C、①②③④ | D、①④ |
考点:空间中直线与平面之间的位置关系
专题:阅读型,空间位置关系与距离
分析:①通过线面垂直的性质和判定,和面面垂直的定义即可判断;②由线面平行的性质和线面垂直的判定,可举反例即可判断;③先通过两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面,再通过面面垂直的判定定理即可得到;④由一直线垂直于两个平行平面中的一个,也垂直于另一个,再由线面垂直的定义即可.
解答:
解:对于①,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m与n相交,且设m与n确定的平面为γ,则γ与α和β的交线所成的角即为α与β所成的角,因为α⊥β,所以由面面垂直的定义知m与n所成的角为90°,故①正确;
②若直线m∥平面α,直线n⊥直线m,则直线n∥平面α或直线n?平面α或直线n⊥平面α,故②错;
③若直线m∥n,m⊥α,则n⊥α,又n?β,故α⊥β,故③正确;
④若平面α∥平面β,直线m⊥平面β,则直线m⊥α,又n?α,故直线m⊥直线n,故④正确.
故选B.
②若直线m∥平面α,直线n⊥直线m,则直线n∥平面α或直线n?平面α或直线n⊥平面α,故②错;
③若直线m∥n,m⊥α,则n⊥α,又n?β,故α⊥β,故③正确;
④若平面α∥平面β,直线m⊥平面β,则直线m⊥α,又n?α,故直线m⊥直线n,故④正确.
故选B.
点评:本题考查空间直线与平面的位置关系,考查直线与平面平行和垂直的判定和性质,掌握这些是迅速解题的关键.

练习册系列答案
相关题目
函数f(x)=ln(x2-x)的定义域为( )
| A、(0,1) |
| B、[0,1] |
| C、(-∞,0)∪(1,+∞) |
| D、(-∞,0]∪[1,+∞) |
已知a>b>0,椭圆C1的方程为
+
=1,双曲线C2的方程为
-
=1,C1与C2的离心率之积为
,则C2的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
如图所示,程序框图(算法流程图)的输出结果是( )
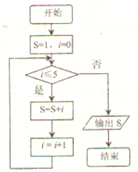

| A、11 | B、15 | C、16 | D、22 |
如图所示,程序框图(算法流程图)的输出结果是( )


| A、22 | B、16 | C、15 | D、11 |
设{an}的首项为a1,公差为-1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|