题目内容
5.半径为2m的圆中,$\frac{π}{3}$的圆心角所对的弧的长度为$\frac{2π}{3}$ m.分析 根据题意可以利用扇形弧长公式l扇形直接计算.
解答 解:根据题意得出:
l扇形=2×$\frac{π}{3}$=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 此题主要考查了扇形弧长的计算,注意掌握扇形的弧长公式是解题关键,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
9.当用反证法证明“已知x>y,证明:x3>y3”时,假设的内容应是( )
| A. | x3≤y3 | B. | x3<y3 | C. | x3>y3 | D. | x3≥y3 |
16.已知以下列联表,且已知P(K2≥6.635)≈0.010,根据此列联表求得随机变量K2的观测值k≈16.373>6.635,那么以下说法正确的是( )
| 患心脏病 | 患其它病 | 总计 | |
| 秃顶 | 214 | 175 | 389 |
| 不秃顶 | 451 | 597 | 1048 |
| 总计 | 665 | 772 | 1437 |
| A. | 秃顶与患心脏病一定有关系 | |
| B. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病有关系 | |
| C. | 我们有1%的把握认为秃顶与患心脏病有关系 | |
| D. | 在犯错误的概率不超过0.010的前提下,认为秃顶与患心脏病没有关系 |
20.直线过点(-3,-2)且在两坐标轴上的截距相等,则该直线方程为( )
| A. | 2x-3y=0 | B. | x+y+5=0 | ||
| C. | 2x-3y=0或x+y+5=0 | D. | x+y+5=0或x-y+1=0 |
15.在平面直角坐标系xOy中,已知△ABC的顶点A(0,4),C(0,-4),顶点B在椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$上,则$\frac{sin(A+C)}{sinA+sinC}$=( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
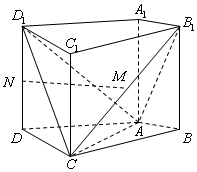 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.