题目内容

20．直线过点（-3，-2）且在两坐标轴上的截距相等，则该直线方程为（　　）
A．2x-3y=0B．x+y+5=0
C．2x-3y=0或x+y+5=0D．x+y+5=0或x-y+1=0

分析 分两种情况考虑，第一：当所求直线与两坐标轴的截距不为0时，设出该直线的方程为x+y=a，把已知点坐标代入即可求出a的值，得到直线的方程；第二：当所求直线与两坐标轴的截距为0时，设该直线的方程为y=kx，把已知点的坐标代入即可求出k的值，得到直线的方程，综上，得到所有满足题意的直线的方程．

解答 解：①当所求的直线与两坐标轴的截距不为0时，设该直线的方程为x+y=a，
把（-3，-2）代入所设的方程得：a=-5，则所求直线的方程为x+y=-5即x+y+5=0；
②当所求的直线与两坐标轴的截距为0时，设该直线的方程为y=kx，
把（-3，-2）代入所求的方程得：k=$\frac{2}{3}$，则所求直线的方程为y=$\frac{2}{3}$x即2x-3y=0．
综上，所求直线的方程为：2x-3y=0或x+y+5=0．
故选：C

点评 此题考查学生会根据条件设出直线的截距式方程和点斜式方程，考查了分类讨论的数学思想，是一道综合题．

练习册系列答案
相关题目
4．一个空间几何体的正视图和侧视图都是边长为1的正三角形，俯视图是一个直径为1的圆，那么这个几何体的全面积为（　　）
A．$\frac{π}{2}$B．$\frac{3π}{4}$C．πD．2π
11．已知函数f（x）=loga（a-k•ax）（a＞0，a≠1）．
（1）当a∈（0，1）时，函数f（x）在[1，+∞）上有意义，求实数k的取值范围；
（2）当a＞1时，若函数f（x）的反函数就是它本身，求k的值及函数f（x）的解析式．
8．如图，已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F恰好是抛物线y2=2px（p＞0）的焦点，且两曲线的公共点连线AB过F，则双曲线的离心率是$\sqrt{2}$+1．
15．某空间几何体的三视图及其尺寸如图所示，则该几何体的表面积是（　　）
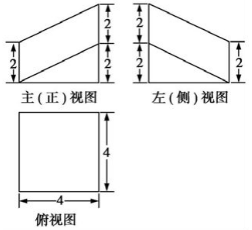
A．32+8$\sqrt{6}$B．48+8$\sqrt{6}$C．48+8$\sqrt{3}$D．44+8$\sqrt{6}$
5．半径为2m的圆中，$\frac{π}{3}$的圆心角所对的弧的长度为$\frac{2π}{3}$ m．
12．计算
（1）lg 8+lg 125-（$\frac{1}{7}$）-2+16${\;}^{\frac{3}{4}}$+（$\sqrt{3}$-1）0
（2）已知tanα=3，求$\frac{2sinα-cosα}{sinα+3cosα}$的值．
9．函数y=log3x的反函数是（　　）
A．y=-log3xB．y=3-xC．y=3xD．y=-3x
10．在△ABC中，已知内角A、B、C所对的边分别为a、b、c，已知$\overrightarrow{m}$=（cosB，cosC），$\overrightarrow{n}$=（2a+c，b）且$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（1）若b=$\sqrt{13}$，a+c=4，求△ABC的面积．
（2）y=sin2A+sin2C的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网