题目内容
已知a，b∈R，且ab≠0．
（I）若ab＞0，求证：
+
≥2；
（Ⅱ）若ab＜0，求证：|
+
|≥2．
（I）若ab＞0，求证：
| b |
| a |
| a |
| b |
（Ⅱ）若ab＜0，求证：|
| b |
| a |
| a |
| b |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用基本不等式，即可证明．
解答：
证明：（I）∵ab＞0，∴
，
＞0，…（2分）
∴
+
≥2
=2，即
+
≥2．…（6分）
（Ⅱ）∵ab＜0，∴
，
＜0，…（8分）
∴|
+
|=(-
)+(-
)≥2
=2，|
+
|≥2．…（12分）
| b |
| a |
| a |
| b |
∴
| b |
| a |
| a |
| b |
|
| b |
| a |
| a |
| b |
（Ⅱ）∵ab＜0，∴
| b |
| a |
| a |
| b |
∴|
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
(-
|
| b |
| a |
| a |
| b |
点评：利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立，这种证明方法叫综合法，即由因导果．利用均值不等式的有关公式最为常见．
练习册系列答案
相关题目
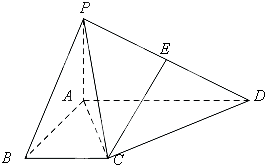如图，四棱锥P-ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC=∠BAD=90°，AD=2PA=2BC=2．
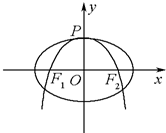如图，抛物线C：y=-