题目内容
设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l⊥m,m在α内,则l⊥α |
| B、若l∥α,l∥m,则m∥α |
| C、若l⊥α,l∥m,则m⊥α |
| D、若l⊥α,l⊥m,则m∥α |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行与垂直的判定定理解决.
解答:
解:l必须垂直于α内的两条相交直线,才能l⊥α,故A错误;
B中,若l∥α,l∥m,则m∥α或m?α,故B错误;
C中,若l⊥α,l∥m,由线面垂直的第二判定定理,我们可得m⊥α,故C正确;
D中,若l⊥α,l⊥m,则m∥α或m?α;
故选:C
B中,若l∥α,l∥m,则m∥α或m?α,故B错误;
C中,若l⊥α,l∥m,由线面垂直的第二判定定理,我们可得m⊥α,故C正确;
D中,若l⊥α,l⊥m,则m∥α或m?α;
故选:C
点评:本题考查线面平行与线面垂直的判定定理的应用.属于基础题.

练习册系列答案
相关题目
若书架上放有的数学,物理,化学书分别是5本,3本,2本,则随机抽出一本是物理书的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=x3+log2x+e-x,则y′=( )
A、
| ||||
B、
| ||||
C、3x2+
| ||||
D、3x2+
|
在△ABC中,a=3,b=6,sinC=
,则△ABC的面积为( )
| ||
| 3 |
A、
| ||
B、2
| ||
C、4
| ||
D、3
|
若 x>0,y>0,且x+y=s,xy=p,则下列命题中正确的是( )
A、当且仅当x=y时s有最小值2
| ||
B、当且仅当x=y时p有最大值
| ||
C、当且仅当p为定值时s有最小值2
| ||
D、若s为定值,当且仅当x=y时p有最大值
|
圆心在直线x=2上的圆C与y轴交于两点A(0,-4),B(0,-2),则圆C的方程为( )
| A、(x-2)2+(y-3)2=5 |
| B、(x-2)2+(y-3)2=25 |
| C、(x-2)2+(y+3)2=5 |
| D、(x-2)2+(y+3)2=25 |
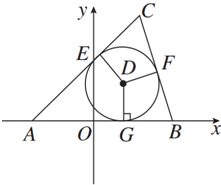 △ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是
△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是