题目内容
15．
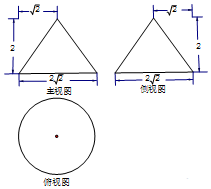某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则新工件的体积为（ ）| A． | $\frac{1}{8}$ | B． | 1 | C． | 2 | D． | $\frac{4π}{3}$ |
分析 依题意知该工件为圆锥，底面半径为$\sqrt{2}$，高为2，要使加工成的正方体新工件体积最大，则该正方体为圆锥的内接正方体，即可得出结论．
解答 解：依题意知该工件为圆锥，底面半径为$\sqrt{2}$，高为2，要使加工成的正方体新工件体积最大，则该正方体为圆锥的内接正方体，设棱长为2x，则有$\frac{\sqrt{2}x}{\sqrt{2}}=\frac{2-2x}{2}$，解得x=$\frac{1}{2}$，故2x=1，故新工件的体积为1．
故选B．
点评 本题考查三视图与直观图的转化，考查学生分析解决问题的能力，确定要使加工成的正方体新工件体积最大，则该正方体为圆锥的内接正方体是关键．
练习册系列答案
相关题目
6．若函数y=2sinωx（ω＞0）在[-$\frac{π}{3}$，$\frac{π}{4}$]上的最小值是-2，但最大值不是2，则ω的取值范围是（ ）
| A． | （0，2） | B． | [$\frac{3}{2}$，2） | C． | （0，$\frac{3}{2}$] | D． | [2，+∞） |
3．数列{an}的各项均为正数，其前n项和为Sn，已知$\frac{n{a}_{n+1}}{{a}_{n}}$$-\frac{（n+1）{a}_{n}}{{a}_{n+1}}$=1，且a1=$\frac{π}{3}$，则tanSn的取值集合是（ ）
| A． | {0，$\sqrt{3}$} | B． | {0，$\sqrt{3}$，$\frac{\sqrt{3}}{3}$} | C． | {0，$\sqrt{3}$，-$\frac{\sqrt{3}}{3}$} | D． | {0，$\sqrt{3}$，-$\sqrt{3}$} |
20．若复数z满足$\frac{zi}{z-i}$=1，其中i为虚数单位，则复数z的模为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 4$\sqrt{2}$ |
4．
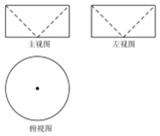如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（ ）
如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |