题目内容
13．从区间[-1，1]内随机取出一个数a，使3a+1＞0的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
分析 本题利用几何概型求概率，首先解得的区间长度以及与区间[-1，1]的长度，求比值即得．
解答 解：由3a+1＞0，解得：a＞-$\frac{1}{3}$，
故满足条件的概率p=$\frac{1+\frac{1}{3}}{1+1}$=$\frac{2}{3}$，
故选：C．
点评 本题主要考查了几何概型，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
相关题目
3．数列{an}的各项均为正数，其前n项和为Sn，已知$\frac{n{a}_{n+1}}{{a}_{n}}$$-\frac{（n+1）{a}_{n}}{{a}_{n+1}}$=1，且a1=$\frac{π}{3}$，则tanSn的取值集合是（ ）
| A． | {0，$\sqrt{3}$} | B． | {0，$\sqrt{3}$，$\frac{\sqrt{3}}{3}$} | C． | {0，$\sqrt{3}$，-$\frac{\sqrt{3}}{3}$} | D． | {0，$\sqrt{3}$，-$\sqrt{3}$} |
4．
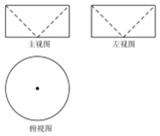如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（ ）
如图是一个几何体挖去另一个几何体所得的三视图，若主视图中长方形的长为2，宽为1，则该几何体的体积为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
1．已知空间四边形ABCD，满足|$\overrightarrow{AB}$|=3，|$\overrightarrow{BC}$|=7，|$\overrightarrow{CD}$|=11，|$\overrightarrow{DA}$|=9，则$\overrightarrow{AC}$•$\overrightarrow{BD}$的值（ ）
| A． | -1 | B． | 0 | C． | $\frac{21}{2}$ | D． | $\frac{33}{2}$ |
8．设全集U=R，集合A={x|x＞0}，B={x|x2-x-2＜0}，则A∩（∁UB）=（ ）
| A． | （0，2] | B． | （-1，2] | C． | [-1，2] | D． | [2，+∞） |
18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上的一点到双曲线的左、右焦点的距离之差为4，若抛物线y=ax2上的两点A（x1，y1），B（x2，y2）关于直线y=x+m对称，且x1x2=-$\frac{1}{2}$，则m的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{5}{2}$ | C． | 2 | D． | 3 |
2．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x-3，x≤1}\\{lnx，x＞1}\end{array}\right.$若|f（x）|+a≥ax，则a的取值范围是（ ）
| A． | [-2，0） | B． | [0，1] | C． | （0，1] | D． | [-2，0] |