题目内容
5.数列{an}的前n项和为Sn,若Sn+an=4-$\frac{1}{{{2^{n-2}}}}({n∈{N^*}})$,则an=$\frac{n}{{2}^{n-1}}$.分析 Sn+an=4-$\frac{1}{{{2^{n-2}}}}({n∈{N^*}})$,n≥2时,Sn-1+an-1=4-$\frac{1}{{2}^{n-3}}$,可得:2an-an-1=$\frac{1}{{2}^{n-2}}$.变形为2n-1an-2n-2an-1=1.利用等差数列的通项公式即可得出.
解答 解:∵Sn+an=4-$\frac{1}{{{2^{n-2}}}}({n∈{N^*}})$,
∴n≥2时,Sn-1+an-1=4-$\frac{1}{{2}^{n-3}}$,
可得:2an-an-1=$\frac{1}{{2}^{n-2}}$.
∴2n-1an-2n-2an-1=1.
n=1时,2a1=4-2,解得a1=1.
∴数列{2n-1an}是等差数列,首项为1,公差为1.
则2n-1an=1+(n-1)=n.
∴an=$\frac{n}{{2}^{n-1}}$.
故答案为:$\frac{n}{{{2^{n-1}}}}$.
点评 本题考查了数列递推公式、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
16.过点P(1,2)的直线l与圆(x-3)2+(y-1)2=5相切,若直线ax+y+3=0与直线l垂直,则a=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{7}$ | D. | 2 |
20.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{x-y+2≥0}\\{2x+y-3≤0}\\{0≤y≤a}\end{array}}\right.$,若 z=-x+2y的最大值为3,则a的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{7}{3}$ |
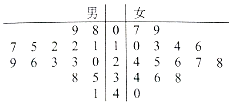 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”. ,集合
,集合 ,
, ,则集合
,则集合 可以表示为( )
可以表示为( ) B.
B.
 D.
D.