题目内容
14．圆x2-2ax+y2=4-a2在y轴上的截距为2，则实数a=$±\sqrt{3}$．分析 令x=0，得y=$±\sqrt{4-{a}^{2}}$，从而2$\sqrt{4-{a}^{2}}$=2，由此能求出a的值．
解答 解：∵圆x2-2ax+y2=4-a2在y轴上的截距为2，
令x=0，得y=$±\sqrt{4-{a}^{2}}$，
∴2$\sqrt{4-{a}^{2}}$=2，解得a=$±\sqrt{3}$．
故答案为：$±\sqrt{3}$．
点评 本题考查实数值的求法，考查圆、截距等基础知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想，是基础题．
练习册系列答案
相关题目
2．下面四个条件中，使a＞b成立的必要而不充分条件是（ ）
| A． | a-1＞b | B． | a+1＞b | C． | |a|＞|b| | D． | a3＞b3 |
9．下列说法正确的是（ ）
| A． | 命题“?x0∈R，2${\;}^{{x}_{0}}$＞1”的否定是“?x∈R，2x≤1” | |
| B． | 命题“若x=y，则x2=y2”的否命题是“若x=y，则x2≠y2” | |
| C． | p：?x∈R，x2+1≥1，q：在△ABC中，若sinA=$\frac{1}{2}$，则A=$\frac{π}{6}$，则p∧q为真命题 | |
| D． | 若平面α⊥平面β，直线a?α，直线b?β，则a⊥b |
19．若复数z满足（z-3）（2-i）=5（i为虚数单位），则z的共轭复数$\overline{z}$为（ ）
| A． | 2+i | B． | 2-i | C． | 5-i | D． | 5+i |
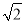，求b，C．