题目内容
8.函数y=ln|x|-x2的图象大致为( )| A. | 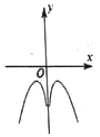 | B. | 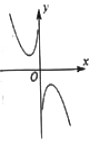 | C. |  | D. | 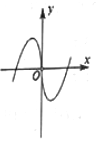 |
分析 先判断函数为偶函数,再根据函数的单调性即可判断.
解答 解:令y=f(x)=ln|x|-x2,其定义域为(-∞,0)∪(0,+∞),
因为f(-x)=ln|x|-x2=f(x),
所以函数y=ln|x|-x2为偶函数,其图象关于y轴对称,故排除B,D,
当x>0时,f(x)=lnx-x2,
所以f′(x)=$\frac{1}{x}$-2x=$\frac{1-2{x}^{2}}{x}$,
当x∈(0,$\frac{\sqrt{2}}{2}$)时,f′(x)>0,函数f(x)递增,
当x∈($\frac{\sqrt{2}}{2}$,+∞)时,f′(x)<0,函数f(x)递减,
故排除C,
方法二:当x→+∞时,函数y<0,故排除C,
故选:A
点评 本题考查了函数的图象的识别,关键掌握函数的奇偶性和函数的单调性,属于中档题.

练习册系列答案
相关题目
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$过点P(4,2),且它的渐近线与圆${({x-2\sqrt{2}})^2}+{y^2}=\frac{8}{3}$相切,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{12}=1$ |
3. 如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )
 如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )
如图是某几何体的三视图,其正视图、俯视图均为直径为2的半圆,则该几何体的表面积为( )| A. | 3π | B. | 4π | C. | 5π | D. | 12π |
18.命题“|x|+|y|≠0”是命题“x≠0或y≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |