题目内容
已知f(x)=(ax+2)6,f′(x)是f(x)导函数,若f′(x)的展开式中x的系数大于f(x)的展开式中x的系数,则a的取值范围是( )
A、a>
| ||
B、0<a<
| ||
C、a>
| ||
D、a>
|
考点:二项式系数的性质,导数的几何意义
专题:二项式定理
分析:清楚还是的导函数,然后求出原函数与导函数展开式x的系数,列出不等式求出a的范围即可.
解答:
解:f(x)=(ax+2)6,f′(x)=6a(ax+2)5,
∴(ax+2)6的展开式中x的系数:
•a•25,
6a(ax+2)5的展开式中x的系数:6a
•a•24,
f′(x)的展开式中x的系数大于f(x)的展开式中x的系数,
所以
•a•25<6a
•a•24,
解得a>
或a<0.
故选:A.
∴(ax+2)6的展开式中x的系数:
| C | 5 6 |
6a(ax+2)5的展开式中x的系数:6a
| C | 4 5 |
f′(x)的展开式中x的系数大于f(x)的展开式中x的系数,
所以
| C | 5 6 |
| C | 4 5 |
解得a>
| 2 |
| 5 |
故选:A.
点评:本题考查二项式定理的应用,函数的导数的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等差数列{an}中,a1=5,前11项和的平均数为55,则a11=( )
| A、15 | B、60 |
| C、100 | D、105 |
若函数f(x)=asinx+
cosx在x=
处有最值,那么a等于( )
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列函数中,在区间(0,+∞)上是增函数的是( )
A、y=
| ||
B、y=
| ||
| C、y=-3x-2 | ||
D、y=(
|
已知a=π
,b=logπ3,c=logπsin
,则a,b,c大小关系为( )
| 1 |
| 2 |
| π |
| 6 |
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c=a>b |
设f(x)与g(x)是定义在R上的两个函数,若对任意x∈[a,b],都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“密切函数”.若f(x)=x2-3x+4与g(x)=2x+t在[2,3]上时“密切函数”,则实数t的取值范围是( )
| A、[-3,-1] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-3,-
|
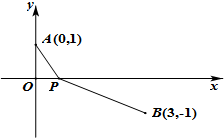 某同学在研究函数f(x)=
某同学在研究函数f(x)=