题目内容
18.已知F1,F2是椭圆C:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左右焦点,点P在椭圆上,且到左焦点F1的距离为6,过F1做∠F1PF2的角平分线的垂线,垂足为M,则OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 延长F1M和PF2交于N,求得椭圆的a=5,运用椭圆的定义和等腰三角形的三线合一,以及三角形的中位线定理,即可得到所求|OM|的值.
解答 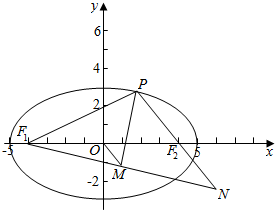 解:延长F1M和PF2交于N,
解:延长F1M和PF2交于N,
椭圆C:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的a=5,
由椭圆的定义可得|PF1|+|PF2|=2a=10,
由|PF1|=6,可得|PF2|=4,
由等腰三角形的三线合一,可得
|PF1|=|PN|=6,
可得|NF2|=6-4=2,
由OM为△F1F2N的中位线,
可得|OM|=$\frac{1}{2}$|F2N|=$\frac{1}{2}$×2=1.
故选A.
点评 本题考查椭圆的定义、方程和性质,考查等腰三角形的性质和三角形的中位线定理的运用,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
6.已知集合A={1,2,3},B={2,3},则( )
| A. | A=B | B. | A∩B=∅ | C. | A⊆B | D. | B⊆A |
3.若数列{an}满足a1=1,a2=2,an=an-1+an-2(n∈N*,n>2),则a6=( )
| A. | 13 | B. | 8 | C. | 21 | D. | 10 |
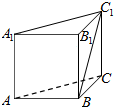 如图,直三棱柱ABC-A1B1C1中(侧棱垂直于底面),∠ABC=90°,且AB=BC=AA1,则BC1与面ACC1A1所成的角的大小为30°.
如图,直三棱柱ABC-A1B1C1中(侧棱垂直于底面),∠ABC=90°,且AB=BC=AA1,则BC1与面ACC1A1所成的角的大小为30°.