题目内容
已知α∈(
,π),sinα=
,则tan(α+
)= .
| π |
| 2 |
| ||
| 5 |
| π |
| 4 |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:依题意,利用同角三角函数间的关系可求得tanα=
=-
,利用两角和的正切即可求得答案.
| sinα |
| cosα |
| 1 |
| 2 |
解答:
解:∵sinα=
,α∈(
,π),
∴cosα=-
=-
,
∴tanα=
=-
,
∴tan(α+
)=
=
=
,
故答案为:
.
| ||
| 5 |
| π |
| 2 |
∴cosα=-
| 1-sin2α |
2
| ||
| 5 |
∴tanα=
| sinα |
| cosα |
| 1 |
| 2 |
∴tan(α+
| π |
| 4 |
| 1+tanα |
| 1-tanα |
1-
| ||
1-(-
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查两角和与差的正切函数,考查同角三角函数间的关系,求得tanα=
=-
是关键,属于中档题.
| sinα |
| cosα |
| 1 |
| 2 |

练习册系列答案
相关题目
偶函数f(x)在区间[-8,-3]上单调递减,则函数f(x)在区间[3,8]上( )
| A、单调递增,且有最小值f(3) |
| B、单调递增,且有最大值f(3) |
| C、单调递减,且有最小值f(8) |
| D、单调递减,且有最大值f(8) |
已知函数f(x)=x2+(m-2)x+m2+12为偶函数,则m的值是( )
| A、1 | B、2 | C、3 | D、4 |
已知一扇形如图,若扇形半径为1,则该扇形的周长等于( )


| A、π+2 | ||
| B、2π | ||
C、
| ||
D、
|
设定义在R上的偶函数f(x)满足f(x+2)=f(x),当x∈[0,1]时,f(x)=x3,则方程f(x)=lg|x|根的个数为( )
| A、12 | B、16 | C、18 | D、20 |
如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
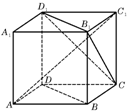

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AC1与CB所成的角为60° |