题目内容
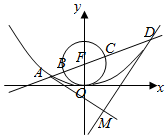
11．抛物线C：x2=2py（p＞0）的焦点为F，l为C的准线，P∈C．且|PF|=6，过P作l的垂线，垂足为M，若△FMP为正三角形，则p=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 根据正三角形的性质，求得丨MF丨=6，∠PMF=$\frac{π}{3}$，则∠FMN=$\frac{π}{6}$，所以p=丨FN丨=3．
解答 
解：设准线l与y轴相交于N，
由|PF|=6，△FMP为正三角形，则丨MF丨=6，∠PMF=$\frac{π}{3}$
由PM⊥l，∠FMN=$\frac{π}{6}$，
∴丨FN丨=3，即p=丨FN丨=3，
∴p=3，
故选：B．
点评 本题考查抛物线的简单几何性质，考查数形结合思想，考查计算能力，属于中档题．
练习册系列答案
相关题目
已知抛物线x2=2py（p＞0）的焦点为F，直线x=4与x轴的交点为P，与抛物线的交点为Q，且$|{QF}|=\frac{5}{4}|{PQ}|$．
6．已知函数f（x）=2cos（ωx+$\frac{3π}{2}$）（ω＞0），若存在m∈[$-\frac{2π}{3}$，0），n∈（0，$\frac{π}{4}$]，使得f（m）-f（n）=0．则实数ω的取值范围为（ ）
| A． | （$\frac{5}{2}$，+∞） | B． | （$\frac{3}{4}$，+∞） | C． | （2，+∞） | D． | （$\frac{3}{2}$，+∞） |
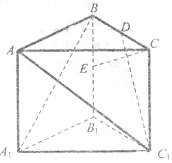在棱长为2的正三棱柱ABC-A1B1C1中，D，E分别是BC，BB1的中点．
B. 
C. 
D. 