题目内容
1.已知函数f(x)=x2+4[sin(θ+$\frac{π}{3}$)]x-2,θ∈[0,2π).(1)若函数f(x)为偶函数,求tanθ的值;
(2)若f(x)在[-$\sqrt{3}$,1]上是单调函数,求θ的取值范围.
分析 (1)由函数为偶函数可得f(-x)-f(x)=0,整理后即可求得θ值,进一步求得tanθ的值;
(2)求出已知二次函数的对称轴方程,结合f(x)在[-$\sqrt{3}$,1]上是单调函数得到关于θ的三角不等式,求解三角不等式得答案.
解答 解:(1)由f(x)=x2+4[sin(θ+$\frac{π}{3}$)]x-2为偶函数,
得f(-x)-f(x)=0,即x2-4[sin(θ+$\frac{π}{3}$)]x-2-x2-4[sin(θ+$\frac{π}{3}$)]x+2=-8[sin(θ+$\frac{π}{3}$)]x=0,
∴sin(θ+$\frac{π}{3}$)=0,
∵θ∈[0,2π),∴θ+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{3}$),
则θ+$\frac{π}{3}$=π或θ+$\frac{π}{3}$=2π,
∴θ=$\frac{2π}{3}$或θ=$\frac{5π}{3}$.
当$θ=\frac{2π}{3}$时,tanθ=$-\sqrt{3}$;当$θ=\frac{5π}{3}$时,tanθ=$-\sqrt{3}$;
(2)函数f(x)=x2+4[sin(θ+$\frac{π}{3}$)]x-2的对称轴方程为x=-2sin(θ+$\frac{π}{3}$),
要使f(x)在[-$\sqrt{3}$,1]上是单调函数,
则-2sin(θ+$\frac{π}{3}$)$≤-\sqrt{3}$或-2sin(θ+$\frac{π}{3}$)≥1,
即sin(θ+$\frac{π}{3}$)$≥\frac{\sqrt{3}}{2}$或sin(θ+$\frac{π}{3}$)$≤-\frac{1}{2}$.
∵θ+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{3}$),
∴θ+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{2π}{3}$]或θ+$\frac{π}{3}$∈[$\frac{7π}{6}$,$\frac{11π}{6}$].
∴θ∈[0,$\frac{π}{3}$]∪[$\frac{5π}{6}$,$\frac{3π}{2}$].
点评 本题考查函数奇偶性与单调性的判定及应用,考查三角函数的图象和性质,属中档题.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | 若p:?x∈R,x2+3x+5>0,则¬p:?x0∈R,x02+3x0+5<0 | |
| B. | “若α=$\frac{π}{3}$,则cosα=$\frac{1}{2}$”的否命题是“若α=$\frac{π}{3}$,则cosα≠$\frac{1}{2}$” | |
| C. | 已知A,B是△ABC的两个内角,则“A>B”是“sinA>sinB”的充要条件 | |
| D. | 命题“p∨q为真”是命题“p∧q为真”的充分不必要条件 |
| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
| A. | 充分但不必要 | B. | 必要但不充分 | ||
| C. | 充分 | D. | 既不充分也不必要 |
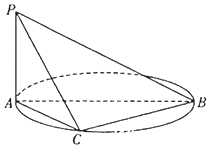 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.