题目内容
6.已知条件p:k=$\sqrt{3}$;条件q:直线y=kx+2与圆x2+y2=1相切,则¬p是¬q的( )| A. | 充分必要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
分析 根据题意,先求出直线y=kx+2与圆x2+y2=1相切时k的值,进而分析可得条件p是条件q的充分不必要条件,结合充要条件的性质可得¬p是¬q的必要不充分条件,即可得答案.
解答 解:根据题意,若直线y=kx+2与圆x2+y2=1相切,
则有$\frac{|2|}{\sqrt{1+{k}^{2}}}$=1,
解可得k=±$\sqrt{3}$,
若有k=$\sqrt{3}$,则有直线y=kx+2与圆x2+y2=1相切,而直线y=kx+2与圆x2+y2=1相切,不一定有k=$\sqrt{3}$,
故条件p:k=$\sqrt{3}$是条件q:直线y=kx+2与圆x2+y2=1相切成立的充分不必要条件,
则¬p是¬q的必要不充分条件,
故选:B.
点评 本题考查充分、必要条件的判定,关键是依据直线与圆的位置关系求出k的值.

练习册系列答案
相关题目
2.点P(-1,2)到直线3x-4y+12=0的距离为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |
11.命题“对任意的x∈R,x2-2x+1≥0”的否定是( )
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 对任意的x∈R,x2-2x+1<0 |
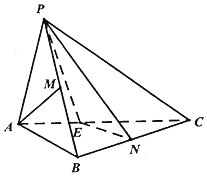 如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.