题目内容
已知圆C的圆心是直线x+y+1=0与直线x-y-1=0的交点，直线3x+4y-1=0与圆C相交于A，B两点，且|AB|=6，则圆C的方程为（ ）
| A、x2+（y+1）2=18 | ||
B、x2+（y-1）2=3
| ||
| C、（x-1）2+y2=18 | ||
D、（x-1）2+y2=3
|
考点：直线与圆相交的性质
专题：直线与圆
分析：求出两直线的交点坐标即圆心坐标，根据相交弦的弦长公式求解半径即可．
解答：
解：直线x+y+1=0与直线x-y-1=0的交点为（0，-1），
∴所以圆C的圆心为C（0，-1），
设半径为r，
由题意可得(
)2+32=r2，
即解得r2=18，
故圆C的方程为x2+（y+1）2=18．
故选：A．
∴所以圆C的圆心为C（0，-1），
设半径为r，
由题意可得(
| |0-4-11| | ||
|
即解得r2=18，
故圆C的方程为x2+（y+1）2=18．
故选：A．
点评：本题主要考查圆的方程的求解根据条件求出圆心和半径是解决本题的关键．考查直线和圆相交的弦长公式的应用．
练习册系列答案
相关题目
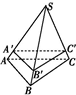已知正棱锥S-ABC的底面边长为4，高为3，在正棱锥内任取一点P，使得VP-ABC＜| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
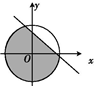区域D是平面直角坐标系中由到原点距离不大于1的点组成，在区域D内任取一点（x，y），该点满足x+y＜
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设f（x）是定义在（0，+∞）上的增函数，当a，b∈（0，+∞）时，均有f（a•b）=f（a）+f（b），已知f（2）=1．求：
（1）f（1）和f（4）的值；
（2）不等式f（x2）＜2f（4）的解集．
（1）f（1）和f（4）的值；
（2）不等式f（x2）＜2f（4）的解集．
某程序框图如图所示，若输出的S=57，则判断框内应填（ ）
| A、k＞4？ | B、k＞5？ |
| C、k＞6？ | D、k＞7？ |