题目内容
已知圆C1的圆心在坐标原点O,且恰好与直线l1:x-y-2
=0相切.
(1)求圆的标准方程;
(2)设点A(x0,y0)为圆上任意一点,AN⊥x轴于N,若动点Q满足
=m
+n
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2.
| 2 |
(1)求圆的标准方程;
(2)设点A(x0,y0)为圆上任意一点,AN⊥x轴于N,若动点Q满足
| OQ |
| OA |
| ON |
考点:轨迹方程
专题:直线与圆
分析:(1)根据直线和圆相切的等价条件求出圆的半径,即可求圆的标准方程;
(2)设出动点Q的坐标,根据向量共线,利用代入法即可求出动点Q的轨迹方程C2.
(2)设出动点Q的坐标,根据向量共线,利用代入法即可求出动点Q的轨迹方程C2.
解答:
解:(1)∵圆C1的圆心在坐标原点O,且恰好与直线l1:x-y-2
=0相切,
∴圆心到直线的距离d=r,
r=
=
=2,
则圆的标准方程为x2+y2=4.
(2)设动点Q(x,y),A(x0,y0),AN⊥x轴,N(x0,0)
由题意(x,y)=m(x0,y0)+n(x0,0),
∴
即
,
将A(x,
y)代入x2+y2=4得
+
=1.
| 2 |
∴圆心到直线的距离d=r,
r=
|0-2
| ||
|
2
| ||
|
则圆的标准方程为x2+y2=4.
(2)设动点Q(x,y),A(x0,y0),AN⊥x轴,N(x0,0)
由题意(x,y)=m(x0,y0)+n(x0,0),
∴
|
即
|
将A(x,
| 1 |
| m |
| x2 |
| 4 |
| y2 |
| 4m2 |
点评:本题主要考查圆的标准方程和与圆有关的轨迹方程的求解,根据条件建立圆心到直线的距离关系以及利用代入法是解决求轨迹问题的基本方法.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2015)的值为( )
| A、-1 | B、1 | C、0 | D、无法确定 |
函数y=
是( )
| 1 | ||
|
| A、(3,+∞)上的增函数 |
| B、[3,+∞)上的增函数 |
| C、(3,+∞)上的减函数 |
| D、[3,+∞)上的增函数 |
已知圆C的圆心是直线x+y+1=0与直线x-y-1=0的交点,直线3x+4y-1=0与圆C相交于A,B两点,且|AB|=6,则圆C的方程为( )
| A、x2+(y+1)2=18 | ||
B、x2+(y-1)2=3
| ||
| C、(x-1)2+y2=18 | ||
D、(x-1)2+y2=3
|
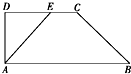 如图所示,在直角梯形ABCD中,AD⊥AB且AB=7,AD=3,CD=4,DE=3,若沿AE折起,使得平面ADE⊥平面ABCE,则四棱锥D-ABCE的外接球的体积为
如图所示,在直角梯形ABCD中,AD⊥AB且AB=7,AD=3,CD=4,DE=3,若沿AE折起,使得平面ADE⊥平面ABCE,则四棱锥D-ABCE的外接球的体积为 期末考试,教师阅卷评分,并检查每个学生成绩,如及格则作“升级”处理,不及格作“留级”处理.将下面的流程图补充完整.
期末考试,教师阅卷评分,并检查每个学生成绩,如及格则作“升级”处理,不及格作“留级”处理.将下面的流程图补充完整.