题目内容
19．若函数f（x）的图象如图所示，则f（x）的解析式可能是（ ）
| A． | $f（x）=\frac{{{e^x}-1}}{{{x^2}-1}}$ | B． | $f（x）=\frac{e^x}{{{x^2}-1}}$ | C． | $f（x）=\frac{{{x^3}+x+1}}{{{x^2}-1}}$ | D． | $f（x）=\frac{{{x^4}+x+1}}{{{x^2}-1}}$ |
分析 由题意，x=0，y＜0，排除A，0＞x＞-1，x→-1，y→-∞，排除C，D选项，f（-2）=5，f（-3）=$\frac{79}{8}$，不符合，排除D，即可得出结论．
解答 解：由题意，x=0，y＜0，排除A，
0＞x＞-1，x→-1，y→-∞，排除C，
D选项中，f（-2）=5，f（-3）=$\frac{79}{8}$，不符合，排除D．
故选：B．
点评 本题考查函数的图象与解析式，考查数形结合的数学思想，正确运用排除法是关键．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
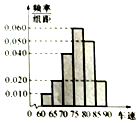交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速（单位：km/h），现将其分成六组为[60，65），[65，70），[70，75），[75，80），[80，85），[85，90]后得到如图所示的频率分布直方图．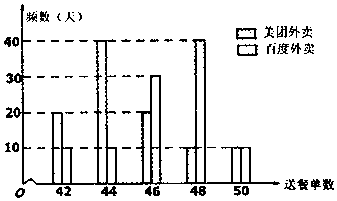
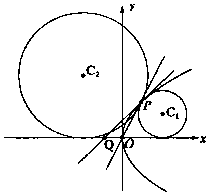如图所示，在直角坐标系xOy中，抛物线C：y2=4x，Q（-1，0），设点P是第一象限内抛物线C上一点，且PQ为抛物线C的切线．
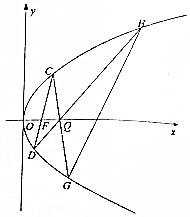在直角坐标系xOy中，设抛物线E：y2=2px（p＞0）的焦点为F，准线为直线l，点A、B在直线l上，点M为抛物线E第一象限上的点，△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形，直线MF的倾斜角为60°．