题目内容
20.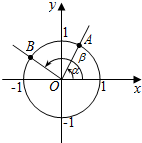 在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.
在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.(Ⅰ)写出cosα,cosβ的值;(只需写出结果)
(Ⅱ)求tanβ的值;
(Ⅲ)求∠AOB的余弦值.
分析 (Ⅰ)利用三角函数的定义,写出cosα,cosβ的值;
(Ⅱ)利用同角三角函数关系求tanβ的值;
(Ⅲ)利用cos∠AOB=cos(β-α)=cosβcosα+sinβsinα,求∠AOB的余弦值.
解答 解:(Ⅰ)$cosα=\frac{5}{13}$;$cosβ=-\frac{4}{5}$.…(2分)
(Ⅱ)因为$cosβ=-\frac{4}{5}$,$\frac{π}{2}<β<π$,
所以$sinβ=\frac{3}{5}$.…(4分)
所以$tanβ=\frac{sinβ}{cosβ}=\frac{{\frac{3}{5}}}{{-\frac{4}{5}}}=-\frac{3}{4}$.…(6分)
(Ⅲ) 因为$cosα=\frac{5}{13}$,$0<α<\frac{π}{2}$,
所以$sinα=\frac{12}{13}$.…(8分)
所以cos∠AOB=cos(β-α)=cosβcosα+sinβsinα=$-\frac{4}{5}×\frac{5}{13}+\frac{3}{5}×\frac{12}{13}$=$\frac{16}{65}$.…(14分)
点评 本题考查三角函数的定义,同角三角函数关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.已知角α的终边经过点$P(-1,\sqrt{3})$,则cosα=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.设正数a,b满足log2a=log3b,则下列结论中,不可能成立的是( )
| A. | 1<a<b | B. | 0<b<a<1 | C. | a=b | D. | 1<b<a |
5.已知i是虚数单位,m,n∈R,则“m=n=1”是“m2-1-2ni=-2i”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.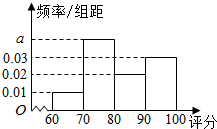 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
(1)求出频率分布与直方图中a的值;
(2)估计这200个零件评分结果的平均数和中位数;
(2)根据已有的经验,可能被修复的零件个体被修复的概率如表:
假设每个零件被修复与否相互独立.现有5个零件的检测指标评分结果为(单位:分):38,43,45,52,58,
①求这5个零件中,至多有2个不被修复而淘汰的概率;
②记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.
 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.(1)求出频率分布与直方图中a的值;
(2)估计这200个零件评分结果的平均数和中位数;
(2)根据已有的经验,可能被修复的零件个体被修复的概率如表:
| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
①求这5个零件中,至多有2个不被修复而淘汰的概率;
②记这5个零件被修复的个数为随机变量X,求X的分布列和数学期望.