题目内容
19.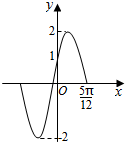 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )| A. | f($\frac{π}{3}$)=1 | |
| B. | 函数f(x)的图象关于x=$\frac{7π}{6}$对称 | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{2}$,0)对称 | |
| D. | 函数f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象 |
分析 由函数图象的顶点的纵坐标求出A,由周期为π可解ω,把点(0,1)代入可解φ的值,从而解得函数解析式,利用正弦函数的图象和性质逐一判断各个选项即可得解.
解答 解:∵由函数图象可得:A=2,
把点(0,1)代入f(x)=Asin(ωx+φ)可得,1=2sinφ,
解得sinφ=$\frac{1}{2}$,又|φ|<$\frac{π}{2}$,故φ=$\frac{π}{6}$,
又∵当x=$\frac{5π}{12}$时,y=0,
∴ω×$\frac{5π}{12}$+$\frac{π}{6}$=π,解得ω=2,
∴f(x)的表达式为:f(x)=2sin(2x+$\frac{π}{6}$),
∴f($\frac{π}{3}$)=2sin(2×$\frac{π}{3}$+$\frac{π}{6}$)=2sin$\frac{5π}{6}$=1,A正确;
由2x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z解得函数的对称轴为x=$\frac{kπ}{2}+\frac{π}{6}$,k∈Z,可得:当k=2时,函数f(x)的图象关于x=$\frac{7π}{6}$对称,B正确;
由2x+$\frac{π}{6}$=kπ,k∈Z解得函数的对称中心坐标为:($\frac{kπ}{2}$-$\frac{π}{12}$,0),k∈Z,由$\frac{kπ}{2}$-$\frac{π}{12}$=-$\frac{11π}{2}$,可得:k=-$\frac{65}{6}$∉Z,故C错误;
由于f(x-$\frac{π}{12}$)=2sin[2(x-$\frac{π}{12}$)+$\frac{π}{6}$]=2sin2x,故D正确.
故选:C.
点评 本题考查根据y=Asin(ωx+∅)的部分图象求其解析式,考查了正弦函数的图象和性质的应用,属于中档题.

| A. | 4 | B. | -4 | C. | 0 | D. | 2 |
| A. | {4,6} | B. | {4} | C. | {6} | D. | ∅ |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
