已知a∈R.“关于x的不等式x2-2ax+a≥0的解集为R 是“0≤a≤1 ( )A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

题目内容

9．已知a∈R，“关于x的不等式x²-2ax+a≥0的解集为R”是“0≤a≤1”（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分也不必要条件

分析不等式x²-2ax+a≥0的解集为R，则△≤0，解出即可．

解答解：关于x的不等式x²-2ax+a≥0的解集为R，
∴△≤0，即4a²-4a≤0，解得0≤a≤1．
∴实数a的取值范围是[0，1]．
故“关于x的不等式x²-2ax+a≥0的解集为R”是“0≤a≤1”的充要条件，
故选：C．

点评本题考查了一元二次不等式的解集与判别式的关系，考查充分必要条件以及学生的运算能力，属于基础题．

练习册系列答案

相关题目

19．

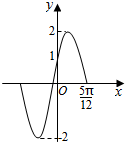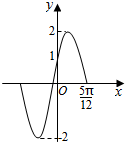已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则下列判断错误的是（　　）

	A．	f（$\frac{π}{3}$）=1
	B．	函数f（x）的图象关于x=$\frac{7π}{6}$对称
	C．	函数f（x）的图象关于（-$\frac{11π}{2}$，0）对称
	D．	函数f（x）的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象

20．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y≥0}\\{2x-y-4≤0}\end{array}\right.$，则目标函数z=2x+y的最大值为（　　）

17．设函数$f（x）=\left\{{\begin{array}{l}{{2^x}，x∈[-1，2]}\\{8-2x，x∈（2，4]}\end{array}}\right.$，则f（-log₂$\sqrt{3}$）=$\frac{\sqrt{3}}{3}$，若f（t）∈[0，1]，则实数t的取值范围是[-1，0]∪[$\frac{7}{2}$，4]．

4．若复数z满足（2+i）z=z+2i，则z=（　　）

14．已知函数$f（x）=3sin（{ωx+\frac{π}{6}}）-2（{ω＞0}）$的图象向右平移$\frac{2π}{3}$个单位后与原图象重合，则ω的最小值是（　　）

1．已知等差数列{a_n}公差为d，前n项和{s_n}，则下列描述不一定正确的是（　　）

	A．	若a₁＞0，d＞0，则n唯一确定时$s_n^{\;}$也唯一确定
	B．	若a₁＞0，d＜0，则n唯一确定时$s_n^{\;}$也唯一确定
	C．	若a₁＞0，d＞0，则$s_n^{\;}$唯一确定时n也唯一确定
	D．	若a₁＞0，d＜0，则$s_n^{\;}$唯一确定时n也唯一确定

18．现有6个白球、4个黑球，任取4个，则至少有两个黑球的取法种数是（　　）

19．已知f（x）=$\frac{a}{3}$x³+$\frac{1}{2}$ax²+x+1无极值点，则a的取值范围．

试题分类