题目内容
4.定义在[-2,2]上的偶函数f(x)在[-2,0]上为增,若满足f(1-m)<f(m),则m的取值范围是$[-1,\frac{1}{2})$.分析 根据偶函数的性质等价转化所求的不等式,利用函数的单调性和定义域,列出关于m的不等式组,再求出m的取值范围.
解答 解:因为f(x)是定义在[-2,2]上的偶函数,
所以不等式f(1-m)<f(m)等价于:f(|1-m|)<f(|m|),
因为f(x)在[-2,0]上为增函数,
所以$\left\{\begin{array}{l}{|1-m|>|m|}\\{-2≤1-m≤2}\\{-2≤m≤2}\end{array}\right.$,解得-1≤m<$\frac{1}{2}$,
即m的取值范围是$[-1,\frac{1}{2})$,
故答案为:$[-1,\frac{1}{2})$.
点评 本题考查函数的奇偶性、单调性的综合应用,正确转化所求的不等式是解题的关键,考查转化思想,注意函数的定义域.

练习册系列答案
相关题目
15.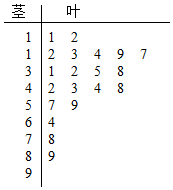 近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
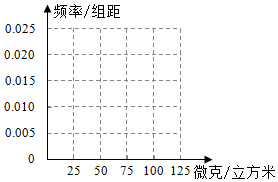
(1)完成如下的频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图;
 (2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
 近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:(1)完成如下的频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图;
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |
 (2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
12.过点(4,0)且斜率为-$\frac{\sqrt{3}}{3}$的直线交圆x2+y2-4x=0于A,B两点,则弦长|AB|等于( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
19.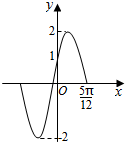 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
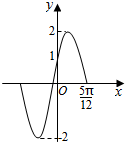 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )| A. | f($\frac{π}{3}$)=1 | |
| B. | 函数f(x)的图象关于x=$\frac{7π}{6}$对称 | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{2}$,0)对称 | |
| D. | 函数f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象 |
9.设命题p:?a>1,函数f(x)=xa(x>0)是增函数,则¬p为( )
| A. | ?a0<1,函数f(x)=xa0(x>0)是减函数 | B. | ?a>1,函数f(x)=xa(x>0)不是减函数 | ||
| C. | ?a0>1,函数f(x)=xa(x>0)不是增函数 | D. | ?a>1,函数f(x)=xa(x>0)是减函数 |
13.从甲、乙、丙、丁四个人中选两名代表,甲被选中的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
14.已知函数$f(x)=3sin({ωx+\frac{π}{6}})-2({ω>0})$的图象向右平移$\frac{2π}{3}$个单位后与原图象重合,则ω的最小值是( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |