题目内容
19．
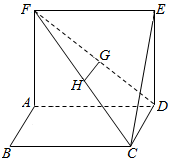如图，四边形ABCD、ADEF为正方形，G，H是DF，FC的中点．（1）求证：GH∥平面CDE；
（2）求证：BC⊥平面CDE．
分析 （1）由中位线定理得出GH∥CD，故GH∥平面CDE；
（2）由AD⊥CD，AD⊥DE得出AD⊥平面CDE，而BC∥AD，故BC⊥平面CDE．
解答 证明：（1）∵G，H是DF，FC的中点．
∴GH∥CD，
又GH?平面CDE，CD?平面CDE，
∴GH∥平面CDE．
（2）∵四边形ABCD、ADEF为正方形，
∴DE⊥AD，CD⊥AD，BC∥AD．
又DE?平面CDE，CD?平面CDE，CD∩DE=D，
∴AD⊥平面CDE，
又BC∥AD，
∴BC⊥平面CDE．
点评 本题考查了线面平行，线面垂直的判定，属于基础题．
练习册系列答案
相关题目
14．
如图，抛物线W：y2=4x与圆C：（x-1）2+y2=25交于A，B两点，点P为劣弧$\widehat{AB}$上不同于A，B的一个动点，与x轴平行的直线PQ交抛物线W于点Q，则△PQC的周长的取值范围是（ ）
如图，抛物线W：y2=4x与圆C：（x-1）2+y2=25交于A，B两点，点P为劣弧$\widehat{AB}$上不同于A，B的一个动点，与x轴平行的直线PQ交抛物线W于点Q，则△PQC的周长的取值范围是（ ）| A． | （10，14） | B． | （12，14） | C． | （10，12） | D． | （9，11） |
4．已知函数f（x）在R上满足f（-x）+f（x）=0，且x＞0时，f（x）=$\frac{1}{2}$（|x+sinα|+|x+2sinα|）+$\frac{3}{2}$sinα（-$\frac{π}{2}$≤α≤$\frac{3π}{2}$）对任意的x∈R，都有f（x-3$\sqrt{3}$）≤f（x）恒成立，则实数α的取值范围为（ ）
| A． | [0，π] | B． | [-$\frac{π}{3}$，$\frac{2π}{3}$] | C． | [-$\frac{π}{6}$，$\frac{7π}{6}$] | D． | [-$\frac{π}{3}$，$\frac{4π}{3}$] |