题目内容
7．已知数列{an}是递增的等差数列，a2，a4是方程x2-6x+8=0的根．（Ⅰ）求{an}的通项公式；
（Ⅱ）求数列{an+2n}的前n项和Sn．
分析 （Ⅰ）通过解方程可知a2=2、a4=4，进而可得公差，计算即得结论；
（Ⅱ）通过（I），利用分组求和法计算即得结论．
解答 解：（Ⅰ）∵a2，a4是方程x2-6x+8=0的根，
∴a2=2、a4=4或a2=4、a4=2（舍），
∴公差d=$\frac{{a}_{4}-{a}_{2}}{4-2}$=1，
∴an=a2+（n-2）d=n；
（Ⅱ）由（I）可知an+2n=n+2n，
∴Sn=（1+2+…+n）+（21+22+…+2n）
=$\frac{n（n+1）}{2}$+$\frac{2（1-{2}^{n}）}{1-2}$
=2n+1-2+$\frac{n（n+1）}{2}$．
点评 本题考查数列的通项及前n项和，考查分组求和法，注意解题方法的积累，属于中档题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
15．已知函数f（x）（x∈R），满足f（-x）=-f（x），f（3-x）=f（x），则f（435）=（ ）
| A． | 0 | B． | 3 | C． | -3 | D． | 不确定 |
18．
银川唐徕回民中学高二年级某次周考中（满分100分），理科A班五名同学的物理成绩如表所示：
（1）请在如图直角坐标系中作出两组数据散点图，并判断正负相关；
（2）依据散点图说明物理成绩与数学成绩是否具有线性相关性，若有，求出线性回归直线方程；
（3）要从4名数学成绩高于90分以上的同学中选出2人参加大学先修课程的学习，求所选两人中至少有一人物理成绩高于90分的概率．
以下公式及数据供选择：
b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=41880；
$\sum_{i=1}^{5}{{x}_{i}}^{2}$=43285．
银川唐徕回民中学高二年级某次周考中（满分100分），理科A班五名同学的物理成绩如表所示：| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x | 89 | 91 | 93 | 95 | 97 |
| 物理y | 87 | 89 | 89 | 92 | 93 |
（2）依据散点图说明物理成绩与数学成绩是否具有线性相关性，若有，求出线性回归直线方程；
（3）要从4名数学成绩高于90分以上的同学中选出2人参加大学先修课程的学习，求所选两人中至少有一人物理成绩高于90分的概率．
以下公式及数据供选择：
b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=41880；
$\sum_{i=1}^{5}{{x}_{i}}^{2}$=43285．
12．为了有效降低工业废气对大气的污染，某厂通过节能降耗技术改造来降低单位产量的能耗，通过统计得到了节能降耗技术改造后生产某产品的产量x（吨）与相应的生产能耗y（吨标准煤）的几组数据如表：
根据如表提供的数据，求出y关于x的回归线方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，其中$\widehat{b}$=0.7，则产量为8吨时相应的生产能耗（吨标准煤）为（ ）
| x | 2 | 3 | 4 | 5 |
| y | 1.5 | 2 | 3 | 3.5 |
| A． | 5.65 | B． | 6.45 | C． | 4.35 | D． | 5.05 |
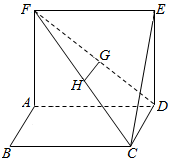如图，四边形ABCD、ADEF为正方形，G，H是DF，FC的中点．
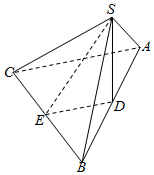如图，在三棱锥S-ABC中，SD⊥平面ABC，D为AB的中点，E为BC的中点，AC=BC．