题目内容
14. 如图,抛物线W:y2=4x与圆C:(x-1)2+y2=25交于A,B两点,点P为劣弧$\widehat{AB}$上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )
如图,抛物线W:y2=4x与圆C:(x-1)2+y2=25交于A,B两点,点P为劣弧$\widehat{AB}$上不同于A,B的一个动点,与x轴平行的直线PQ交抛物线W于点Q,则△PQC的周长的取值范围是( )| A. | (10,14) | B. | (12,14) | C. | (10,12) | D. | (9,11) |
分析 由抛物线定义可得|QC|=xQ+1,从而△PQC的周长=|QC|+|PQ|+|PC|=xQ+1+(xP-xQ)+5=6+xP,联立圆的方程和抛物线的方程,确定P点横坐标的范围,即可得到结论.
解答 解:抛物线的准线l:x=-1,焦点C(1,0),
由抛物线定义可得|QC|=xQ+1,
圆(x-1)2+y2=25的圆心为(1,0),半径为5,
可得△PQC的周长=|QC|+|PQ|+|PC|=xQ+1+(xP-xQ)+5=6+xP,
由抛物线y2=4x及圆(x-1)2+y2=25可得交点的横坐标为4,
即有xP∈(4,6),
可得6+xP∈(10,12),
故△PQC的周长的取值范围是(10,12).
故选:C.
点评 本题考查抛物线的定义,考查抛物线与圆的位置关系,确定P点横坐标的范围是关键,属于中档题.

练习册系列答案
相关题目
2.方程x2-y2=-1表示( )
| A. | 焦点在x轴的双曲线 | B. | 圆 | ||
| C. | 两条直线 | D. | 焦点在y轴的双曲线 |
5.在平面几何中有正确的结论,已知一个正三角形的内切圆面积为S1,外接圆面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{4}$,类比上述结论推理,在空间中,已知一个正四面体的内切球体积为V1,外接球体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{27}$ |
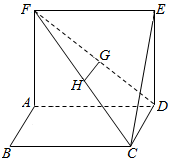 如图,四边形ABCD、ADEF为正方形,G,H是DF,FC的中点.
如图,四边形ABCD、ADEF为正方形,G,H是DF,FC的中点.