题目内容
已知函数f(x)=sin2x+sin2x+3cos2x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求函数的单调减区间;
(Ⅲ)当x∈[-
,
]时,求函数f(x)的最小值.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求函数的单调减区间;
(Ⅲ)当x∈[-
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)化简解析式可得f(x)=
sin(2x+
),即可求出f(x)的最小正周期.
(Ⅱ)由
+2kπ≤2x+
≤
+2kπ即可求得函数的单调减区间.
(Ⅲ)由已知可先求得2x+
的范围,即可求出函数f(x)的最小值.
| 2 |
| π |
| 4 |
(Ⅱ)由
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
(Ⅲ)由已知可先求得2x+
| π |
| 4 |
解答:
(本题10分)
解:(Ⅰ)∵f(x)=sin2x+2cos2x+1=sin2x+cos2x=
sin(2x+
),…(2分)
∴f(x)的最小正周期T=
=π.…(4分)
(Ⅱ)由
+2kπ≤2x+
≤
+2kπ得
+kπ≤x≤
+kπ(k∈Z)
∴函数的单调减区间[
+kπ,
+kπ](k∈Z).…(7分)
(Ⅲ)由x∈[-
,
]⇒2x∈[-
,
]⇒2x+
∈[-
,
].
∴当2x+
=-
时,即x=-
时,f(x)取得最小值0.…(10分)
解:(Ⅰ)∵f(x)=sin2x+2cos2x+1=sin2x+cos2x=
| 2 |
| π |
| 4 |
∴f(x)的最小正周期T=
| 2π |
| ω |
(Ⅱ)由
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
∴函数的单调减区间[
| π |
| 8 |
| 5π |
| 8 |
(Ⅲ)由x∈[-
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴当2x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
点评:本题主要考察了三角函数中的恒等变换应用,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
相关题目
如果△A1B1C1的三个内角的余弦值分别为△A2B2C2的三个内角的正弦值,则△A1B1C1一定是锐角三角形,△A2B2C2一定是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
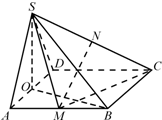 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求证:平面SOB⊥平面SCM.
已知圆C:(x-2)2+y2=1和两点A(0,a)与B(0,-a)(a>0),若圆C上存在一点P使得PA⊥PB,则a的取值范围是( )
| A、(0,3] |
| B、(0,1] |
| C、[1,3] |
| D、[3,+∞) |