题目内容
设α,β为锐角,且(1+sinα-cosα)(1+sinβ-cosβ)=2sinαsinβ,则α+β= .
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系,二倍角公式、两角和的正切公式求得tan(α+β)=1,结合α,β为锐角,可得α+β 的值.
解答:
解:∵
=
=1+tan
,同理可得
=1+tan
,
∴由(1+sinα-cosα)(1+sinβ-cosβ)=2sinαsinβ 可得
•
=2,
∴(1+tan
)(1+tan
)=1+tan
+tan
+tan
tan
=2,
tan
+tan
=1-tan
tan
,故tan
=
=1,
∴
=
,α+β=
故答案为:
.
| 1+sinα-cosα |
| sinα |
sinα+2sin2
| ||
| sinα |
| α |
| 2 |
| 1+sinβ-cosβ |
| sinβ |
| β |
| 2 |
∴由(1+sinα-cosα)(1+sinβ-cosβ)=2sinαsinβ 可得
| 1+sinα-cosα |
| sinα |
| 1+sinβ-cosβ |
| sinβ |
∴(1+tan
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
tan
| α |
| 2 |
| β |
| 2 |
| α |
| 2 |
| β |
| 2 |
| α+β |
| 2 |
tan
| ||||
1-tan
|
∴
| α+β |
| 2 |
| π |
| 4 |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题主要考查同角三角函数的基本关系,二倍角公式,两角和的正切公式,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
某棱柱如图所示放置,则该棱柱的正视图是( )


A、 |
B、 |
C、 |
D、 |
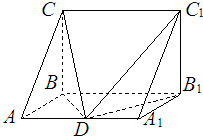 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,BC=