题目内容
已知函数f（x）=x3-3x+a有三个零点，则a的取值范围为（ ）
| A、（-∞，-2）∪（2，+∞） |
| B、（-∞，2]∪[2，+∞） |
| C、（-2，2） |
| D、[-2，2] |
考点：利用导数研究函数的极值,函数零点的判定定理
专题：函数的性质及应用
分析：已知条件转化为函数有两个极值点，并且极小值小于0，极大值大于0，求解即可．
解答：
解：由函数f（x）=x3-3x+a有三个不同的零点，
则函数f（x）有两个极值点，极小值小于0，极大值大于0；
由f′（x）=3x2-3=3（x+1）（x-1）=0，解得x1=1，x2=-1，
所以函数f（x）的两个极，x∈（-∞，-1），f′（x）＞0，x∈（-1，1），f′（x）＜0，x∈（1，+∞），f′（x）＞0，
∴函数的极小值f（1）=a-2和极大值f（-1）=a+2．
因为函数f（x）=x3-3x+a有三个不同的零点，
所以
，解之，得-2＜a＜2．
故实数a的取值范围是（-2，2）．
故选：C
则函数f（x）有两个极值点，极小值小于0，极大值大于0；
由f′（x）=3x2-3=3（x+1）（x-1）=0，解得x1=1，x2=-1，
所以函数f（x）的两个极，x∈（-∞，-1），f′（x）＞0，x∈（-1，1），f′（x）＜0，x∈（1，+∞），f′（x）＞0，
∴函数的极小值f（1）=a-2和极大值f（-1）=a+2．
因为函数f（x）=x3-3x+a有三个不同的零点，
所以
|
故实数a的取值范围是（-2，2）．
故选：C
点评：本题是中档题，考查函数的导数与函数的极值的关系，考查转化思想，计算能力．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
下列命题正确的是（ ）
| A、如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面 |
| B、如果直线a和平面α满足a∥α，那么a与α内的任何直线平行 |
| C、如果直线a，b和平面α满足a∥α，b∥α，那么a∥b |
| D、如果直线a，b和平面α满足a∥b，a∥α，b?α，那么b∥α |
函数f（x）=x2-ax+2在（2，+∞）上单调递增，则a的取值范围为（ ）
| A、[2，+∞） |
| B、[4，+∞） |
| C、（-∞，4] |
| D、（-∞，-4] |
“x=2”是“log2|x|=1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f（x）=lg
的图象（ ）
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
在平面直角坐标系xOy中，椭圆E：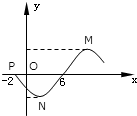
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的图象的一部分如图，已知函数与x轴交于点P（-2，0）和（6，0），点M，N分别是最高点和最低点，且∠MPN=