题目内容
10.第二象限角的集合表示为{x|$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z}.分析 先确定第二象限角的边界,再由终边相同角的定义写出所求角的集合.
解答 解:第二象限角是角的终边落在y轴非负半轴,以及x轴的非负半轴之间所有的角,
故第二象限角的集合为{x|$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z},
故答案为:{x|$\frac{π}{2}$+2kπ<α<π+2kπ,k∈Z},
点评 本题考查终边相同角的定义和象限角的定义,注意确定角的集合的边界.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
20.在同一平面内,线段AB为圆C的直径,动点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$>0,则点P与圆C的位置关系是( )
| A. | 点P在圆C外部 | B. | 点P在圆C上 | C. | 点P在圆C内部 | D. | 不确定 |
18.不等式(x+3)(1-x)≥0的解集为( )
| A. | {x|-3≤x≤1} | B. | {x|x≥3或x≤-1} | C. | {x|-1≤x≤3} | D. | {x|x≤-3或x≥1} |
20.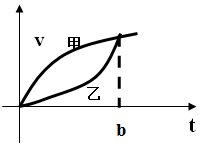 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )| A. | a甲(b)>a乙(b),S甲(b)>S乙(b) | B. | a甲(b)<a乙(b),S甲(b)<S乙(b) | ||
| C. | a甲(b)<a乙(b),S甲(b)>S乙(b) | D. | a甲(b)<a乙(b),S甲(b)<S乙(b) |
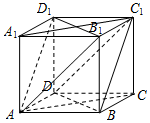 已知正方体ABCD-A1B1C1D1棱长为a.
已知正方体ABCD-A1B1C1D1棱长为a.