题目内容
9.设α为锐角,若$cos(α+\frac{π}{6})=\frac{3}{5}$,则$sin(α-\frac{π}{6})$=$\frac{4-3\sqrt{3}}{10}$.分析 根据同角的三角函数的关系和两角差的正弦公式即可求出.
解答 解:∵0<α<$\frac{π}{2}$,
∴$\frac{π}{6}$$<α+\frac{π}{6}$<$\frac{2π}{3}$,
∵$cos(α+\frac{π}{6})=\frac{3}{5}$,
∴sin($α+\frac{π}{6}$)=$\frac{4}{5}$,
∵$sin(α-\frac{π}{6})$=sin(α+$\frac{π}{6}$-$\frac{π}{3}$)=sin(α+$\frac{π}{6}$)cos$\frac{π}{3}$-cos(α+$\frac{π}{6}$)sin$\frac{π}{3}$=$\frac{4}{5}$×$\frac{1}{2}$-$\frac{3}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$,
故答案为:$\frac{4-3\sqrt{3}}{10}$
点评 本题考查了同角的三角函数的关系和两角差的正弦公式,属于基础题.

练习册系列答案
相关题目
2.-1060o的终边落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.某地区根据2008年至2014年每年的生活垃圾无害化处理量y(单位:万吨)的数据,用线性回归模型拟合y关于t的回归方程为:$\widehat{y}$=0.92+0.1t(t表示年份代码,自2008年起,t的取值分别为1,2,3…),则下列表述不正确的是( )
| A. | 自2008年起,每年的生活垃圾无害化处理量和年份代码正相关 | |
| B. | 自2008年起,每年的生活垃圾无害化处理量大约增加0.10万吨 | |
| C. | 由此模型可知2016年该地区生活垃圾无害化处理量是1.82万吨 | |
| D. | 由此模型预测出2017年该地区生活垃圾无害化处理量约为1.92万吨 |
1.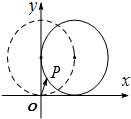 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )| A. | (1-sin1,1-cos1) | B. | (1+sin1,1-cos1) | C. | (1-sin1,1+cos1) | D. | (1+sin1,1+cos1) |