题目内容
14.正△ABP的顶点A(0,a)(a>0)为定点,顶点B在x轴上移动,且顶点A、B、P的顺序是逆时针方向,求顶点P的轨迹.分析 设点B、P的坐标分别为(t,0)、(x,y),则复数AB=t-ai,复数AP=x+(y-a)i,利用复数知识求解即可得出结论.
解答 解:设点B、P的坐标分别为(t,0)、(x,y),则复数AB=t-ai,复数AP=x+(y-a)i,
∴x+(y-a)i=(t-ai)(($\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)=$\frac{1}{2}$(t+$\sqrt{3}$a)+$\frac{1}{2}$($\sqrt{3}$t-a)i,
∴x=$\frac{1}{2}$(t+$\sqrt{3}$a),y=$\frac{1}{2}$($\sqrt{3}$t+a),消去t得:$\sqrt{3}$x-y=a.
此即点P的轨迹方程,点P的轨迹是倾斜角为60°,在y轴上截距为-a的直线.
点评 本题考查轨迹与轨迹方程,考查复数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.已知点P(a,b),Q(c,d),则方程$\left\{\begin{array}{l}{x=\frac{a+ct}{1+t}}\\{y=\frac{b+dt}{1+t}}\end{array}\right.$(t为参数)表示的曲线是( )
| A. | 直线PQ | B. | 线段PQ | C. | 除去P点的直线PQ | D. | 除去Q点的直线PQ |
2.存在函数f(x)满足对任意的x∈R都有( )
| A. | f(|x|)=x+1 | B. | f(x2+4x)=|x+2| | C. | f(2x2+1)=x | D. | f(cosx)=$\sqrt{x}$ |
19.用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<n(n∈N,且n>1)时,不等式的左边从n=k到n=k+1,需添加的式子是( )
| A. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}-1}$ | B. | $\frac{1}{{2}^{k+1}-1}$ | ||
| C. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k+1}-1}$ | D. | $\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+…+$\frac{1}{{2}^{k+1}-1}$ |
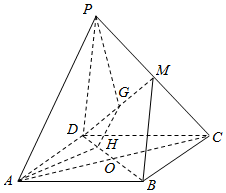 如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.
如图,P是菱形ABCD所在平面外一点,∠BAD=60°,△PCD是等边三角形,AB=2,PA=2$\sqrt{2}$,M是PC的中点,点G为线段DM上一点(端点除外),平面APG与BD交于点H.