题目内容
19.用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<n(n∈N,且n>1)时,不等式的左边从n=k到n=k+1,需添加的式子是( )| A. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+$\frac{1}{{2}^{k}+2}$+…+$\frac{1}{{2}^{k+1}-1}$ | B. | $\frac{1}{{2}^{k+1}-1}$ | ||
| C. | $\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k+1}-1}$ | D. | $\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+…+$\frac{1}{{2}^{k+1}-1}$ |
分析 分别写出n=k、n=k+1时不等式左边的表达式,然后相减即得结论.
解答 解:当n=k时,左边=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$,
当n=k+1时,左边=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{k}-1}$+$\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$,
两式相减得:$\frac{1}{{2}^{k}}$+…+$\frac{1}{{2}^{k+1}-1}$,
故选:A.
点评 本题考查数学归纳法,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.复数$\frac{2+i}{1-2i}$( )
| A. | i | B. | -i | C. | 4+2i | D. | 1+i |
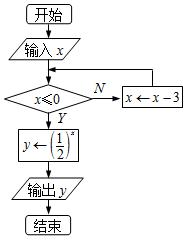 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.