题目内容
3.直线l过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点F,且与此椭圆交于点A,B,若椭圆上存在一点M,使得$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OM}$(O为坐标原点).(1)求椭圆的离心率的取值范围;
(2)椭圆上是否存在这样一点M,使得四边形OAMB为矩形,如果存在,试求出M的坐标;如果不存在,请说明理由.
分析 (1)设F(c,0),直线l的方程为y=k(x-c),代入椭圆方程,运用韦达定理和向量的加法坐标运算,代入椭圆方程,解方程可得k,由k2>0,解不等式可得e的范围;
(2)椭圆上假设存在这样一点M,使得四边形OAMB为矩形.即有OA⊥OB,可得x1x2+y1y2=0,代入韦达定理,化简整理,解得k,结合(1),即可得到矛盾,进而判断不存在.
解答 解:(1)设F(c,0),直线l的方程为y=k(x-c),
代入椭圆方程可得(b2+a2k2)x2-2ca2k2x+a2c2k2-a2b2=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=$\frac{2c{a}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,x1x2=$\frac{{a}^{2}{c}^{2}{k}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,
y1+y2=k(x1+x2-2c)=-$\frac{2kc{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,
由$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OM}$,可得M的坐标为($\frac{2c{a}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,-$\frac{2kc{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$),
代入椭圆方程可得
$\frac{4{c}^{2}{a}^{2}{k}^{4}}{({b}^{2}+{a}^{2}{k}^{2})^{2}}$+$\frac{4{k}^{2}{c}^{2}{b}^{2}}{({b}^{2}+{a}^{2}{k}^{2})^{2}}$=1,
即有k4(4c2a2-a4)+k2(4c2b2-2a2b2)-b4=0,
△=(4c2b2-2a2b2)2+4b4(4c2a2-a4)
=16c4b4,
解得k2=$\frac{{a}^{2}{b}^{2}}{4{c}^{2}{a}^{2}-{a}^{4}}$或$\frac{{a}^{2}{b}^{2}-4{c}^{2}{b}^{2}}{4{c}^{2}{a}^{2}-{a}^{4}}$=-$\frac{{b}^{2}}{{a}^{2}}$(舍去),
由k2>0,可得4c2a2-a4>0,
即为c>$\frac{1}{2}$a,可得$\frac{1}{2}$<e<1;
(2)椭圆上假设存在这样一点M,使得四边形OAMB为矩形.
即有OA⊥OB,可得x1x2+y1y2=0,
即有(1+k2)x1x2-ck2(x1+x2)+k2c2=0,
由(1)可得(1+k2)•$\frac{{a}^{2}{c}^{2}{k}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$-ck2($\frac{2c{a}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$)+k2c2=0,
化简可得k2=$\frac{{a}^{2}{b}^{2}}{{a}^{2}{c}^{2}-{b}^{4}}$,
由(1)可得k2=$\frac{{a}^{2}{b}^{2}}{4{c}^{2}{a}^{2}-{a}^{4}}$,
即有a2c2-b4=4a2c2-a4,
即为3a2c2=(a2-b2)(a2+b2),
即有2a2=b2,这与a>b矛盾,
故不存在这样一点M,使得四边形OAMB为矩形.
点评 本题考查椭圆的离心率的范围,注意运用联立直线方程和椭圆方程,运用韦达定理和向量的加法运算,考查存在性问题的解法,注意运用两向量垂直的条件:数量积为0,考查化简整理的运算能力,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | 8+4π | B. | 4+4π | C. | 8+2π | D. | 4+2π |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
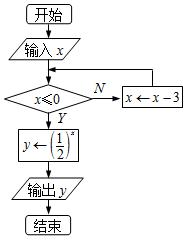 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.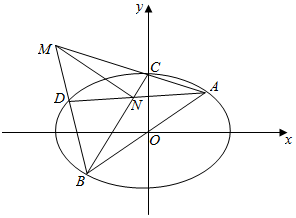 如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.
如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.