题目内容
6.一个袋子中有k个红球,4个绿球,2个黄球,这些球除颜色外其他完全相同.从中一次随机取出2个球,每取得1个红球记1分、取得1个绿球记2分、取得1个黄球记5分,用随机变量X表示取到2个球的总得分,已知总得分是2分的概率为$\frac{1}{12}$.(Ⅰ)求袋子中红球的个数;
(Ⅱ)求X的分布列和数学期望.
分析 (Ⅰ)当取到的2个球都是红球时,总得分是2分,从而$P(X=2)=\frac{C_k^2}{{C_{k+6}^2}}=\frac{1}{12}$,由此能求出袋子中有3个红球.
(Ⅱ)依题意,X的所有可能取值为2,3,4,6,7,10,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 (本题13分)
解:(Ⅰ)当取到的2个球都是红球时,总得分是2分,
即$P(X=2)=\frac{C_k^2}{{C_{k+6}^2}}=\frac{1}{12}$,…(2 分)
化简得11k2-23k-30=0,即(k-3)(11k+10)=0,…(3 分)
解得k=3或$k=-\frac{10}{11}$(舍去).
故袋子中有3个红球.…(4 分)
(Ⅱ)依题意,X的所有可能取值为2,3,4,6,7,10.…(5 分)
$P(X=2)=\frac{1}{12}$,
$P(X=3)=\frac{C_3^1C_4^1}{C_9^2}=\frac{3×4}{36}=\frac{1}{3}$,
$P(X=4)=\frac{C_4^2}{C_9^2}=\frac{6}{36}=\frac{1}{6}$,
$P(X=6)=\frac{C_3^1C_2^1}{C_9^2}=\frac{3×2}{36}=\frac{1}{6}$,
$P(X=7)=\frac{C_4^1C_2^1}{C_9^2}=\frac{4×2}{36}=\frac{2}{9}$,
$P(X=10)=\frac{C_2^2}{C_9^2}=\frac{1}{36}$.…(10分)
∴X的分布列为:
| X | 2 | 3 | 4 | 6 | 7 | 10 |
| P | $\frac{1}{12}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{2}{9}$ | $\frac{1}{36}$ |
$E(X)=2×\frac{1}{12}+3×\frac{1}{3}+4×\frac{1}{6}+6×\frac{1}{6}+7×\frac{2}{9}+10×\frac{1}{36}=\frac{14}{3}$.…(13分)
点评 本题考查概率的求法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
16.已知函数f(x)的定义域为R,对任意x1<x2,有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>-1,且f(1)=1,则不等式f(log2|3x-1|)<2-log2|3x-1|的解集为( )
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,0)∪(0,3) | D. | (-∞,0)∪(0,1) |
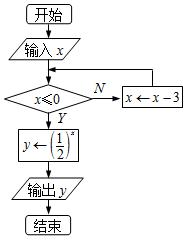 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.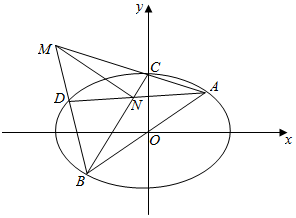 如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.
如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.