题目内容
2.存在函数f(x)满足对任意的x∈R都有( )| A. | f(|x|)=x+1 | B. | f(x2+4x)=|x+2| | C. | f(2x2+1)=x | D. | f(cosx)=$\sqrt{x}$ |
分析 根据函数解析式,举特殊值,计算函数值,可判断A,C,D均不恒成立,可得B正确.
解答 解:A项,当x=1时,f(1)=2;当x=-1时,f(1)=0,不合题意;
C项,当x=1时,f(3)=1;当x=-1时,f(3)=-1,不合题意;
D项,当x=0时,f(1)=1;当x=2π时,f(1)=$\sqrt{2π}$,不合题意;
故选B.
点评 本题考察了函数的定义域性质,解析式,特值法求解函数的问题,关键举反例得出结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.某几何体的正视图和侧(左)视图都是边长为2的正方体,俯视图是扇形,体积为2π,该几何体的表面积为( )
| A. | 8+4π | B. | 4+4π | C. | 8+2π | D. | 4+2π |
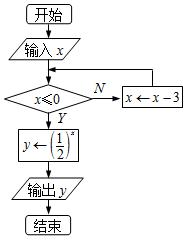 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.