题目内容
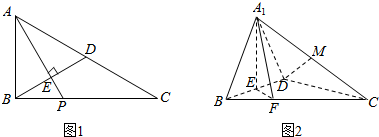
6.如图1,在△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F.将△ABD沿BD折起,得到三棱锥A1-BCD,如图2所示.(Ⅰ)若M是A1C的中点,求证:DM∥平面A1EF;
(Ⅱ)若平面A1BD⊥平面BCD,试判断直线A1B与直线CD能否垂直?并说明理由.
分析 (Ⅰ)取FC中点N,推导出DN∥EF,MN∥A1F,由此能证明DM∥平面A1EF.
(Ⅱ)推导出EF⊥平面A1BD,从而A1B⊥EF,假设A1B⊥CD,则A1B⊥平面BCD,A1E⊥平面BCD,与“过一点和已知平面垂直的直线只有一条”相矛盾,从而直线A1B与直线CD不能垂直.
解答  (本小题满分13分)
(本小题满分13分)
证明:(Ⅰ)取FC中点N.
在图1中,由D,N分别为AC,FC中点,
所以DN∥EF.(2分)
在图2中,由M,N分别为A1C,FC中点,
所以MN∥A1F,(4分)
所以平面DMN∥平面A1EF,(5分)
所以DM∥平面A1EF.(6分)
解:(Ⅱ)直线A1B与直线CD不可能垂直.(7分)
因为平面A1BD⊥平面BCD,EF?平面BCD,EF⊥BD,
所以EF⊥平面A1BD,(8分)
所以A1B⊥EF.(9分)
假设有A1B⊥CD,
注意到CD与EF是平面BCD内的两条相交直线,
则有A1B⊥平面BCD.(1)(10分)
又因为平面A1BD⊥平面BCD,A1E?平面A1BD,A1E⊥BD,
所以A1E⊥平面BCD.(2)(11分)
而(1),(2)同时成立,这显然与“过一点和已知平面垂直的直线只有一条”相矛盾,
所以直线A1B与直线CD不可能垂直.(13分)
点评 本题考查线面平行的证明,考查两直线是否垂直的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
11.设x,y满足约束条件$\left\{\begin{array}{l}y-x≤1\\ x+y≤3\\ y≥m\end{array}\right.$,若z=x+3y的最大值与最小值的差为7,则实数m=( )
| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
15.函数y=2sin(2πx)的图象与直线y=x的交点个数为( )
| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
 如图,棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.
如图,棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.
 某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.
某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系$t=\left\{\begin{array}{l}64,x≤0\\{2^{kx+6}},x>0.\end{array}\right.$且该食品在4℃的保鲜时间是16小时.