题目内容
11．设x，y满足约束条件$\left\{\begin{array}{l}y-x≤1\\ x+y≤3\\ y≥m\end{array}\right.$，若z=x+3y的最大值与最小值的差为7，则实数m=（ ）| A． | $\frac{3}{2}$ | B． | $-\frac{3}{2}$ | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |
分析 由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，进一步求出最值，结合最大值与最小值的差为7求得实数m的值．
解答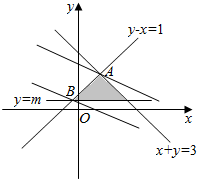 
解：由约束条件$\left\{\begin{array}{l}y-x≤1\\ x+y≤3\\ y≥m\end{array}\right.$作出可行域如图，
联立$\left\{\begin{array}{l}{y-x=1}\\{x+y=3}\end{array}\right.$，解得A（1，2），
联立$\left\{\begin{array}{l}{y=m}\\{y-x=1}\end{array}\right.$，解得B（m-1，m），
化z=x+3y，得$y=-\frac{x}{3}+\frac{z}{3}$．
由图可知，当直线$y=-\frac{x}{3}+\frac{z}{3}$过A时，z有最大值为7，
当直线$y=-\frac{x}{3}+\frac{z}{3}$过B时，z有最小值为4m-1，
由题意，7-（4m-1）=7，解得：m=$\frac{1}{4}$．
故选：C．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
1．已知某圆锥曲线C的极坐标方程是ρ2=$\frac{225}{9+16co{s}^{2}θ}$，则曲线C的离心率为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{5}{3}$ | D． | $\frac{5}{4}$ |
19．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$的两个焦点分别为F1，F2，|F1F2|=2c（c＞0）．若点P在椭圆上，且∠F1PF2=90°，则点P到x轴的距离为（ ）
| A． | $\frac{b^2}{a}$ | B． | $\frac{b^2}{c}$ | C． | $\frac{c^2}{a}$ | D． | $\frac{c^2}{b}$ |
如图，在△ABC中，∠ABC=90°，AB=3，BC=4，点O为BC的中点，以BC为直径的半圆与AC，AO分别相交于点M，N，则AN=$\sqrt{13}-2$；$\frac{AM}{MC}$=$\frac{9}{16}$．
3．设集合A={x|x＞a}，集合B={-1，1，2}，若A∩B=B，则实数a的取值范围是（ ）
| A． | （1，+∞） | B． | （-∞，1） | C． | （-1，+∞） | D． | （-∞，-1） |