题目内容
函数f（x）=log
(4x-x2)的递减区间为 ．
| 1 |
| 2 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：根据复合函数单调性之间的关系即可得到结论．
解答：
解：由4x-x2＞0，即x2-4x＜0，解得0＜x＜4，即函数的定义域为（0，4），
设t=4x-x2，则函数y=log
t为减函数，
要求函数f（x）的递减区间，根据复合函数单调性之间的关系，即求函数t=4x-x2的增区间，
∵函数t=4x-x2的对称轴为x=2，
∴t=4x-x2的增区间为（0，2），
∴f（x）=log
(4x-x2)的递减区间为（0，2），
故答案为：（0，2）
设t=4x-x2，则函数y=log
| 1 |
| 2 |
要求函数f（x）的递减区间，根据复合函数单调性之间的关系，即求函数t=4x-x2的增区间，
∵函数t=4x-x2的对称轴为x=2，
∴t=4x-x2的增区间为（0，2），
∴f（x）=log
| 1 |
| 2 |
故答案为：（0，2）
点评：本题主要考查函数单调区间的求解，根据复合函数单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
函数f（x）=ax-2+loga（x-1）（a＞0且a≠1），在x∈[2，3]上的最大值与最小值之和为a，则a等于（ ）
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
已知集合M={x∈R|（x+1）（x-2）＞0}和N={x∈R|x2+x＜0}，则集合M是集合N的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
三个数a=0.22，b=log202，c=20.1之间的大小关系是（ ）
| A、a＜c＜b |
| B、a＜b＜c |
| C、b＜a＜c |
| D、b＜c＜a |
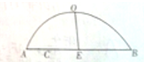如图，A处为我军一炮兵阵地，距A处1000米的C处有一小山，山高为580米，在山的另一侧距C处3000米有敌武器库B，且A、B、C在同一水平直线删个，已知我炮兵轰击敌武器库是一段抛物线，这段抛物线的最大高度OE为800米．