题目内容
 已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)证明:BN⊥平面C1B1N;
(2)求二面角B1-CN-A的正弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由题意∠BNB1为直角,B1C1⊥BN,由此能证明BN⊥面C1B1N.
(2)以B为原点,BA为x轴,BB1为y轴,BC为z轴,建立空间直角坐标系,利用向量法能求出二面角B1-CN-A的正弦值.
(2)以B为原点,BA为x轴,BB1为y轴,BC为z轴,建立空间直角坐标系,利用向量法能求出二面角B1-CN-A的正弦值.
解答:
(1)证明:由题意:该几何体的正视图其正视图为矩形,
侧视图为等腰直角三角形,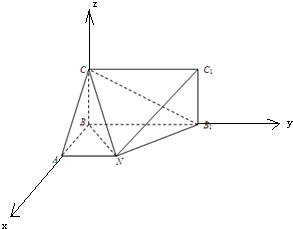
俯视图为直角梯形.
则B1C1⊥面ABB1N,且在ABB1N内,
∴∠BNB1为直角
∵B1C1⊥面ABB1N且BN?面ABB1N,
∴B1C1⊥BN,又∵BN⊥B1N,且B1N∩B1C1=B1,
∴BN⊥面C1B1N
(2)解:以B为原点,BA为x轴,BB1为y轴,
BC为z轴,建立空间直角坐标系,
由已知得B1(0,8,0),C(0,0,4),
N(4,4,0),A(4,0,0),
=(4,4,-4),
=(0,8,-4),
=(4,0,-4),
设平面CNB1的法向量
=(x,y,z),
则
,
取y=1,得
=(1,1,2),
设平面CNA的法向量
=(a,b,c),
则
,
取a=1,得
=(1,0,1),
设二面角B1-CN-A的平面角为θ.
则cosθ=
=
,∴sinθ=
=
.
∴二面角B1-CN-A的正弦值为
.
侧视图为等腰直角三角形,

俯视图为直角梯形.
则B1C1⊥面ABB1N,且在ABB1N内,
∴∠BNB1为直角
∵B1C1⊥面ABB1N且BN?面ABB1N,
∴B1C1⊥BN,又∵BN⊥B1N,且B1N∩B1C1=B1,
∴BN⊥面C1B1N
(2)解:以B为原点,BA为x轴,BB1为y轴,
BC为z轴,建立空间直角坐标系,
由已知得B1(0,8,0),C(0,0,4),
N(4,4,0),A(4,0,0),
| CN |
| CB1 |
| CA |
设平面CNB1的法向量
| m |
则
|
取y=1,得
| m |
设平面CNA的法向量
| n |
则
|
取a=1,得
| n |
设二面角B1-CN-A的平面角为θ.
则cosθ=
| ||||
|
|
| ||
| 2 |
1-
|
| 1 |
| 2 |
∴二面角B1-CN-A的正弦值为
| 1 |
| 2 |
点评:本题考查直线与平面垂直的证明,考查二面角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知Sn是等差数列{an}n∈N*的前n项和,且S6>S7>S5,给出下列五个命题:
①d<0;②S11>0;③S12<0;④数列{Sn}中最大项为S11;⑤|a6|>|a7|,
其中正确命题的个数( )
①d<0;②S11>0;③S12<0;④数列{Sn}中最大项为S11;⑤|a6|>|a7|,
其中正确命题的个数( )
| A、5 | B、4 | C、3 | D、1 |
已知集合M={x∈R|(x+1)(x-2)>0}和N={x∈R|x2+x<0},则集合M是集合N的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
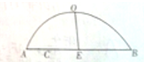 如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.
如图,A处为我军一炮兵阵地,距A处1000米的C处有一小山,山高为580米,在山的另一侧距C处3000米有敌武器库B,且A、B、C在同一水平直线删个,已知我炮兵轰击敌武器库是一段抛物线,这段抛物线的最大高度OE为800米.